题目内容
2.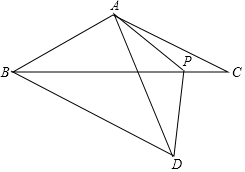 如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.
如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.(1)当点P由点C运动到点B时,求运动过程中∠PBD的大小;
(2)请求出在(1)情况下点D运动的路径长度.
分析 (1)①如图1中,在BC上截取一点F,使得BF=AF,当点P在点F左侧时,可证∠PBD=∠DAP=30°.②当点P与F重合时,∠PBD不存在,当点P在点F右侧时,如图2中,可证∠PBD=∠ABD+∠ABC=150°;
(2)如图3中,易知,点D的运动轨迹是线段DD′.求出BD,BD′即可解决问题;
解答 解:(1)①如图1中,在BC上截取一点F,使得BF=AF,当点P在点F左侧时,
∵AB=AC,PA=PD,∠BAC=∠APD=120°,
∴∠ABP=∠ADP=30°,
∵∠ABO=∠PDO=30°,∠AOB=∠POD,
∴△AOB≌△POD,
∴$\frac{BO}{OD}$=$\frac{OA}{OP}$,
∴$\frac{BO}{OA}$=$\frac{OD}{OP}$,∵∠BOD=∠AOP,
∴△BOD∽△AOP,
∴∠PBD=∠DAP=30°.
②当点P与F重合时,∠PBD不存在,当点P在点F右侧时,如图2中,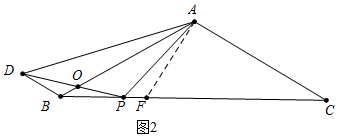
同法由△AOD∽△POB,推出△BOD∽△POA,可得∠DBO=∠APD=120°,
∴∠PBD=∠ABD+∠ABC=150°,
∴当点P由点C运动到点B时,∠PBD的值为30°或120°或不存在.
(2)如图3中,易知,点D的运动轨迹是线段DD′.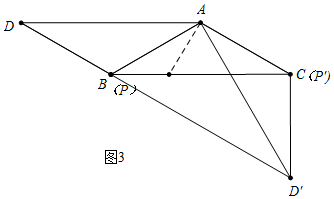
易知BD=AB=4,BD′=2AB=8,
∴DD′=BD+BD′=12.
点评 本题考查轨迹、解直角三角形、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x2-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.
如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x2-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.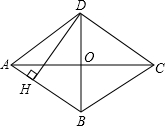 如图所示,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB 于点H,且DH与AC交于点G,则AH的长是多少?
如图所示,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB 于点H,且DH与AC交于点G,则AH的长是多少?