题目内容
13．要使式子$\sqrt{x+1}$有意义，x的取值范围是（ ）| A． | x≠1 | B． | x≠-1 | C． | x≥1 | D． | x≥-1 |
分析 根据被开方数大于等于0列不等式求解即可．
解答 解：由题意得，x+1≥0，
解得x≥-1．
故选D．
点评 本题考查了二次根式有意义的条件，二次根式中的被开方数必须是非负数，否则二次根式无意义．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
4．已知$\frac{a}{b}$=$\frac{2}{3}$，则$\frac{a}{a+b}$的值为（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{5}{2}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
1．
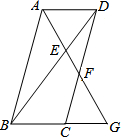如图，在?ABCD中，G为BC延长线的一点，连结AG交对角线BD于E，交CD于F，下面结论错误的是（ ）
如图，在?ABCD中，G为BC延长线的一点，连结AG交对角线BD于E，交CD于F，下面结论错误的是（ ）| A． | $\frac{EA}{EG}$=$\frac{AD}{BG}$ | B． | $\frac{DE}{BE}$=$\frac{FD}{FG}$ | C． | $\frac{CF}{CG}$=$\frac{CD}{BG}$ | D． | $\frac{AD}{BG}$=$\frac{AF}{AG}$ |
8．已知整数a1，a2，a3，a4…满足下列条件：a1=0，a2=-|a1+1|，a3=-|a2+2|，a4=-|a3+3|…依此类推，则a2017的值为（ ）
| A． | -1009 | B． | -1008 | C． | -2017 | D． | -2016 |
18．
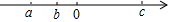已知有理数a、b、c在数轴上对应的点的位置如图所示，化简$\frac{a}{|a|}$-$\frac{a-c}{|a-c|}$+$\frac{|b|}{b}$的结果为（ ）
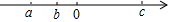已知有理数a、b、c在数轴上对应的点的位置如图所示，化简$\frac{a}{|a|}$-$\frac{a-c}{|a-c|}$+$\frac{|b|}{b}$的结果为（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
3．下列四个标志中，是轴对称图形的是图（ ）
| A． |  | B． |  | C． |  | D． |  |