题目内容
1.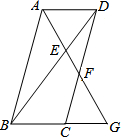 如图,在?ABCD中,G为BC延长线的一点,连结AG交对角线BD于E,交CD于F,下面结论错误的是( )
如图,在?ABCD中,G为BC延长线的一点,连结AG交对角线BD于E,交CD于F,下面结论错误的是( )| A. | $\frac{EA}{EG}$=$\frac{AD}{BG}$ | B. | $\frac{DE}{BE}$=$\frac{FD}{FG}$ | C. | $\frac{CF}{CG}$=$\frac{CD}{BG}$ | D. | $\frac{AD}{BG}$=$\frac{AF}{AG}$ |
分析 由四边形ABCD是平行四边形,可得AD∥BC,AB∥CD,则可判定△AED∽△GEB,△ADF∽△GCF∽△GBA,△ABE∽△FDE,再根据相似三角形的性质解答即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴△AED∽△GEB,△ADF∽△GCF∽△GBA,△ABE∽△FDE,
∴$\frac{EA}{EG}=\frac{AD}{BG},\frac{DE}{BE}=\frac{AE}{EG},\frac{CF}{CG}=\frac{CD}{BG},\frac{AD}{BG}=\frac{AF}{AG}$,
故选B
点评 此题考查了相似三角形的判定与平行四边形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
12.若y=kx-4的函数值y随x的增大而减小,则k的值可能是下列的( )
| A. | -4 | B. | 0 | C. | 1 | D. | 3 |
9.已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数y=$\frac{2}{x}$的图象上的三点,且x1<x2<0<x3,则y1、y2、y3的大小关系是 ( )
| A. | y3<y2<y1 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
6.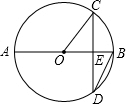 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,DB,若∠CDB=30°,⊙O的半径为4$\sqrt{3}$cm,则弦CD的长为( )| A. | 8$\sqrt{3}$cm | B. | 12cm | C. | 6$\sqrt{3}$cm | D. | 8cm |
13.要使式子$\sqrt{x+1}$有意义,x的取值范围是( )
| A. | x≠1 | B. | x≠-1 | C. | x≥1 | D. | x≥-1 |
10.|-2|的倒数是( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | -2 | D. | $\frac{1}{2}$ |
11.已知∠A=55°34′,则∠A的余角等于( )
| A. | 44°26′ | B. | 44°56′ | C. | 34°56′ | D. | 34°26′ |
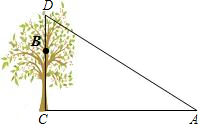 如图,一棵树CD,在其6m高的点B处有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树12m处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处.如果两只猴子所经过的路程相等,试问这棵树有多高?
如图,一棵树CD,在其6m高的点B处有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树12m处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处.如果两只猴子所经过的路程相等,试问这棵树有多高?


