题目内容
a是不为1的有理数,我们把
称为a的差倒数,如:2的差倒数是
=-1.已知a1=-
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…依此类推,那么a2015= .
| 1 |
| 1-a |
| 1 |
| 1-2 |
| 1 |
| 3 |
考点:规律型:数字的变化类
专题:
分析:把
称为a的差倒数,已知a1=-
,可依次计算出a2、a3、a4、a5,即可发现每3个数为一个循环,然后用2015除以3,根据规律,即可得出答案.
| 1 |
| 1-a |
| 1 |
| 3 |
解答:解:∵a1=-
,
∴a2=
=
,
a3=
=4,
a4=
=-
,
…
-
,
,4每3个数一循环,
依此类推,2015÷3=671…2,
所以a2015=a2=
.
故答案为:
| 1 |
| 3 |
∴a2=
| 1 | ||
1-(-
|
| 3 |
| 4 |
a3=
| 1 | ||
1-
|
a4=
| 1 |
| 1-4 |
| 1 |
| 3 |
…
-
| 1 |
| 3 |
| 3 |
| 4 |
依此类推,2015÷3=671…2,
所以a2015=a2=
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:此题主要考查学生对倒数和数字变化类知识点的理解和掌握,解答此题的关键是依次计算出a2、a3、a4、a5,找出数字变化的规律.

练习册系列答案
相关题目
4个小朋友在一起,每两人握一次手,他们一共握了6次手,12个小朋友在一起,他们一共握手的次数是( )
| A、18 | B、60 | C、66 | D、144 |
下列各式中计算结果为零的是( )
| A、-22+(-2)2 |
| B、-22-22 |
| C、-22-(-2)2 |
| D、-(-2)2-(-2)2 |
将4个红球、3个白球、2个黑球放入一个不透明的袋子里,从中摸出8个球,恰好红球、白球、黑球都摸到,这个事件是( )
| A、必然事件 | B、不可能事件 |
| C、随机事件 | D、不能确定 |
 如图,正方形ABCD的边长为2,E是BC的中点,F是对角线BD上的一个动点(点F不与B、D重合).设EF+FC的长为x,则x的取值范围是
如图,正方形ABCD的边长为2,E是BC的中点,F是对角线BD上的一个动点(点F不与B、D重合).设EF+FC的长为x,则x的取值范围是 如图1,AB=12cm,点C在线段AB上,点M、N分别是AC、BC的中点.
如图1,AB=12cm,点C在线段AB上,点M、N分别是AC、BC的中点.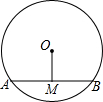 如图,⊙O的弦AB=9,M是AB的中点,且OM为3,则⊙O的半径为
如图,⊙O的弦AB=9,M是AB的中点,且OM为3,则⊙O的半径为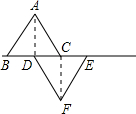 如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.
如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.