题目内容
如图，正方形ABCD的边长为2，E是BC的中点，F是对角线BD上的一个动点（点F不与B、D重合）．设EF+FC的长为x，则x的取值范围是考点：轴对称-最短路线问题,正方形的性质
专题：
分析：求得EF+FC的最大值和最小值即可求得取值范围．
解答：解：当A，F，E在一条直线时，x取得最小值，
此时连接AE交BD于F，有EF+FC=AE=
，
当F于D重合时，x取得最大值，
此时EF+FC=CD+DE=2+
，
因为点F不与B、D重合，
所以x的取值范围是
≤x＜2+
．
此时连接AE交BD于F，有EF+FC=AE=
| 5 |
当F于D重合时，x取得最大值，
此时EF+FC=CD+DE=2+
| 5 |
因为点F不与B、D重合，
所以x的取值范围是
| 5 |
| 5 |
点评：本题考查了正方形的性质，轴对称-最短路线问题，求得最小值和最大值是关键．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，D为BC上的一点，AD=BD=2，AB=2| 3 |
A、
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
将数轴上表示-5的点，先向右移动两个单位长度，再向左移动三个单位长度后对应的点表示的数是（ ）
| A、-1 | B、-4 | C、4 | D、-6 |
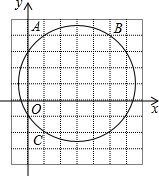如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，4），（5，4），（1，-2），则以A，B，C为顶点的三角形外接圆的圆心坐标是（ ）| A、（2，3） |
| B、（3，2） |
| C、（3，1） |
| D、（1，3） |
如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，已知点A的坐标为（-4，2），请解答下列问题；
如图，点D、E在△ABC的边BC上，BE=DC，AD=AE，求证：AB=AC．