Question

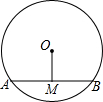如图，⊙O的弦AB=9，M是AB的中点，且OM为3，则⊙O的半径为

 

．

Answer 1

考点：垂径定理,勾股定理

专题：

分析：连接OA，根据垂径定理求出AM的长和∠OMA=90°，根据勾股定理求出AO，即可得出答案．

解答：解：连接OA，
∵⊙O的弦AB=9，M是AB的中点，
∴OM⊥AB，AM=BM=

9

2

，
∴∠OMA=90°，
∵OM为3，
∴由勾股定理得：AO=

( 9 2 )2+32

=

73

2

，
故答案为：

73

2

．

点评：本题考查了垂径定理和勾股定理的应用，解此题的关键是求出AM长，注意：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧，难度适中．