题目内容
已知抛物线y=x2-4x+k的顶点A在直线y=-4x+4上,抛物线与直线y=-4x+4的另一交点为B,抛物线与x轴交于C、D两点﹙C在左侧﹚.求:
(1)抛物线的顶点坐标;
(2)点B的坐标;
(3)S△ABC;
(4)四边形ABCD的面积和S△ABD.
(1)抛物线的顶点坐标;
(2)点B的坐标;
(3)S△ABC;
(4)四边形ABCD的面积和S△ABD.
考点:抛物线与x轴的交点,二次函数的性质
专题:计算题
分析:(1)由抛物线解析式求出顶点横坐标,代入直线y=-4x+4中求出纵坐标,即可确定出顶点坐标;
(2)由顶点坐标确定出k的值,进而确定出抛物线解析式,与y=-4x+4联立求出B坐标即可;
(3)如图所示,连接BC,AC,由直线AB解析式求出E坐标,得到CE的长,三角形ABC面积=三角形BCE面积+三角形ACE面积,求出即可;
(4)连接BD,AD,三角形ABD面积=三角形BED面积+三角形AED面积,再由三角形ABD面积+三角形ABC面积求出四边形ACBD面积即可.
(2)由顶点坐标确定出k的值,进而确定出抛物线解析式,与y=-4x+4联立求出B坐标即可;
(3)如图所示,连接BC,AC,由直线AB解析式求出E坐标,得到CE的长,三角形ABC面积=三角形BCE面积+三角形ACE面积,求出即可;
(4)连接BD,AD,三角形ABD面积=三角形BED面积+三角形AED面积,再由三角形ABD面积+三角形ABC面积求出四边形ACBD面积即可.
解答: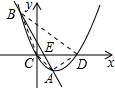 解:(1)抛物线y=x2-4x+k=(x-2)2+k-4,
解:(1)抛物线y=x2-4x+k=(x-2)2+k-4,
∴顶点横坐标为2,
将x=2代入得:y=-4x+4=-4,
则顶点坐标为(2,-4);
(2)将(2,-4)代入抛物线解析式得:-4=4-8+k,
解得:k=0,即抛物线解析式为y=x2-4x,
联立得:
,
解得:
或
,
则B(-2,12);
(3)如图所示,连接AC,BC,设直线AB与x轴交于E点,
对于抛物线y=x2-4x=x(x-4),
令y=0,得到x=0或x=4,即C(0,0),D(4,0),
对于直线y=-4x+4,令y=0,得到x=1,即直线y=-4x+4与x轴交点E为(1,0),
则S△ABC=S△BCE+S△ACE=
×1×12+
×1×4=6+2=8;
(4)连接BD,AD,
∵CD=4,CE=1,
∴ED=CD-CE=3,
∴S△ABD=S△BED+S△AED=
×3×12+
×3×4=18+6=24;
则S四边形ACBD=8+24=32.
 解:(1)抛物线y=x2-4x+k=(x-2)2+k-4,
解:(1)抛物线y=x2-4x+k=(x-2)2+k-4,∴顶点横坐标为2,
将x=2代入得:y=-4x+4=-4,
则顶点坐标为(2,-4);
(2)将(2,-4)代入抛物线解析式得:-4=4-8+k,
解得:k=0,即抛物线解析式为y=x2-4x,
联立得:
|
解得:
|
|
则B(-2,12);
(3)如图所示,连接AC,BC,设直线AB与x轴交于E点,
对于抛物线y=x2-4x=x(x-4),
令y=0,得到x=0或x=4,即C(0,0),D(4,0),
对于直线y=-4x+4,令y=0,得到x=1,即直线y=-4x+4与x轴交点E为(1,0),
则S△ABC=S△BCE+S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
(4)连接BD,AD,
∵CD=4,CE=1,
∴ED=CD-CE=3,
∴S△ABD=S△BED+S△AED=
| 1 |
| 2 |
| 1 |
| 2 |
则S四边形ACBD=8+24=32.
点评:此题考查了抛物线与x轴的交点,以及二次函数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方的B点.已知易拉罐底面周长是12cm,高是5cm,那么所需彩带最短是多少?
如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方的B点.已知易拉罐底面周长是12cm,高是5cm,那么所需彩带最短是多少? 如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD.
如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD. 如图:点A的坐标是(2,2),点P是x轴正半轴上的一个动点,若△AOP是等腰三角形,求P点的坐标.
如图:点A的坐标是(2,2),点P是x轴正半轴上的一个动点,若△AOP是等腰三角形,求P点的坐标. 如图,△ABC中,∠ABC和∠ACB的平分线BE,CF相交于点G.求证:
如图,△ABC中,∠ABC和∠ACB的平分线BE,CF相交于点G.求证: 如图,在梯形ABCD中,AD∥BC,AB=DC,梯形的周长为16cm,∠B=30°.设高AH为x(cm),中位线EF的长为y(cm),求y关于x的函数关系式,并求出自变量x的取值范围.
如图,在梯形ABCD中,AD∥BC,AB=DC,梯形的周长为16cm,∠B=30°.设高AH为x(cm),中位线EF的长为y(cm),求y关于x的函数关系式,并求出自变量x的取值范围. 如图,AE=AF,点B、D分别在AE、AF上,四边形ABCD是菱形,连接EC、FC
如图,AE=AF,点B、D分别在AE、AF上,四边形ABCD是菱形,连接EC、FC