题目内容
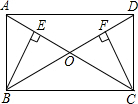 如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于E,CF⊥BD于F.
如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于E,CF⊥BD于F.(1)线段BE与CF相等吗?请说明理由;
(2)当AB=2,∠AOB=60°时,求BE的值.
考点:矩形的性质
专题:
分析:(1)根据矩形的对角线互相平分且相等可得OB=OC,再利用“角角边”证明△BOE和△COF全等,然后利用全等三角形对应边相等证明;
(2)求出△AOB是等边三角形,再根据等边三角形的性质求解即可.
(2)求出△AOB是等边三角形,再根据等边三角形的性质求解即可.
解答:(1)证明:在矩形ABCD中,OA=OB=OC,
∵BE⊥AC,CF⊥BD,
∴∠BEO=∠CFO=90°,
在△BOE和△COF中,
,
∴△BOE≌△COF(AAS),
∴BE=CF;
(2)∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴BE=
AB=2×
=
.
∵BE⊥AC,CF⊥BD,
∴∠BEO=∠CFO=90°,
在△BOE和△COF中,
|
∴△BOE≌△COF(AAS),
∴BE=CF;
(2)∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴BE=
| ||
| 2 |
| ||
| 2 |
| 3 |
点评:本题考查了矩形的性质,等边三角形的判定与性质,全等三角形的判定与性质,熟记性质并确定出全等三角形是解题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
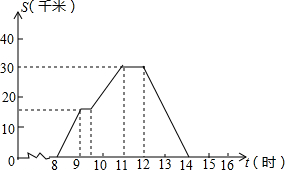 一天上午8:00时,小华去县城购物,到下午14:00时返回家,设他离家的距离为s千米,结合图象回答:
一天上午8:00时,小华去县城购物,到下午14:00时返回家,设他离家的距离为s千米,结合图象回答: 在图中,这些方砖除颜色外完全相同,小老鼠在方砖上自由走动,最终停在白色方砖上的概率为
在图中,这些方砖除颜色外完全相同,小老鼠在方砖上自由走动,最终停在白色方砖上的概率为