题目内容
5.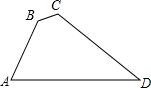 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )| A. | $6\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $4\sqrt{2}$ | D. | $4\sqrt{3}$ |
分析 过点A,D分别作AE,DF垂直于直线BC,垂足分别为E,F,根据∠B=135°,∠C=120°,可构成等腰直角三角形,和角是30°的直角三角形,根据其性质,可求出线段AG,DG长,根据勾股定理可求出AD的长.
解答 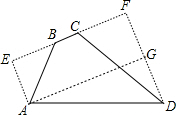 解:如图,过点A,D分别作AE,DF垂直于直线BC,垂足分别为E,F.
解:如图,过点A,D分别作AE,DF垂直于直线BC,垂足分别为E,F.
∵∠B=135°,
∴∠ABE=45°,
∴BE=AE=$\frac{\sqrt{2}}{2}$×$\sqrt{6}$=$\sqrt{3}$,
∵∠C=120°,
∴∠DCF=60°,
∵CD=6,
∴CF=6cos60°=6×$\frac{1}{2}$=3,
∴DF=6sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴EF=$\sqrt{3}$+(3-$\sqrt{3}$)+3=6.
过点A作AG⊥DF,垂足为G.在Rt△ADG中,AG=EF=6,DG=DF-AE=3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$.
根据勾股定理得AD=$\sqrt{A{G}^{2}+D{G}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.
故选D.
点评 本题考查了勾股定理的应用,和等腰直角三角形的性质和30°直角三角形的特点,从而可求出解.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.若x2-5x+6=(x+a)(x+b),a,b的值可能为( )
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
10.有一锐角相等的两个直角三角形一定( )
| A. | 全等 | B. | 相似 | ||
| C. | 既不全等也不相似 | D. | 相似但不全等 |
 一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.
一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.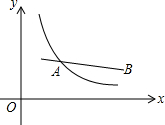 如图,已知线段AB,点A的坐标为(1,$\frac{3}{2}$),点B的坐标为(4,1),反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB有交点,则k的取值范围为$\frac{3}{2}$≤k≤4.
如图,已知线段AB,点A的坐标为(1,$\frac{3}{2}$),点B的坐标为(4,1),反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB有交点,则k的取值范围为$\frac{3}{2}$≤k≤4.