题目内容
2.用分组分解法分解因式.(1)4xy+1-4x2-y2;
(2)xz-yz-x2+2xy-y2;
(3)a4b-a2b3+a3b2-ab4;
(4)25y2-4a2-12ab-9b2;
(5)a2b2-a2-b2-4ab+1.
分析 (1)先分组,再根据完全平方公式和平方差公式分解即可;
(2)先分组,再提公因式即可;
(3)先分组,再提公因式、运用平方差公式分解即可;
(4)先分组,再根据完全平方公式和平方差公式分解即可;
(5)先分组,再根据完全平方公式和平方差公式分解即可.
解答 解:(1)4xy+1-4x2-y2=1-(4x2-4xy+y2)=1-(2x-y)2=(1+2x-y)(1-2x+y);
(2)xz-yz-x2+2xy-y2=z(x-y)-(x-y)2=(x-y)(z-x+y);
(3)a4b-a2b3+a3b2-ab4=a2b(a2-b2)+ab2(a2-b2)=ab(a+b)2(a-b);
(4)25y2-4a2-12ab-9b2=25y2-(4a2+12ab+9b2)=25y2-(2a+3b)2=(5y+2a+3b)(5y-2a-3b);
(5)a2b2-a2-b2-4ab+1=(ab-1)2-(a+b)2=(ab-1+a+b)(ab-1-a-b).
点评 本题考查的是多项式的因式分解,灵活运用分组分解法进行因式分解是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
10.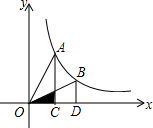 如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
 如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
8. 如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是( )
如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是( )
 如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是( )
如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是( )| A. | BF=DF | B. | ∠1=∠EFD | C. | BF>EF | D. | FD∥BC |
 拿一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF,如果∠DFE=65°,则∠DFA=50度.
拿一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF,如果∠DFE=65°,则∠DFA=50度.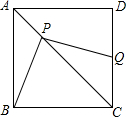 如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4$\sqrt{2}$,CQ=10,则正方形ABCD的面积为324.
如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4$\sqrt{2}$,CQ=10,则正方形ABCD的面积为324. 如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且CD=$\frac{1}{2}$AB,DE⊥CF于E.求证:CE=EF.
如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且CD=$\frac{1}{2}$AB,DE⊥CF于E.求证:CE=EF.