题目内容
3.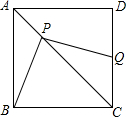 如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4$\sqrt{2}$,CQ=10,则正方形ABCD的面积为324.
如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4$\sqrt{2}$,CQ=10,则正方形ABCD的面积为324.
分析 作PM⊥BC于点M,PN⊥CD于点N,利用正方形的性质和角平分线上的点到角的两边相等以及已知条件即可证明△BPM≌△QPN,得出BM=QN,设BM=x,则NF=x,PM=CM=CN=10+x,根据平行线分线段成比例定理即可得到关于x的比例式,求出x的值,即可求出正方形的边长,进而求出其面积.
解答 解:作PM⊥BC于点M,PN⊥CD于点N,如图所示: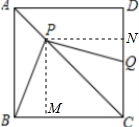
∵四边形ABCD是正方形,
∴AC平分∠BCD,
∴PM=PN,∠NEM=90°,
∴四边形PMCN为正方形,∵PQ⊥BP,∴∠BPQ=90°,
∴∠BPM=∠NPQ,
在△BPM和△QPN中,$\left\{\begin{array}{l}{∠BMP=∠QNP}&{\;}\\{∠BPM=∠QPN}&{\;}\\{PM=PN}&{\;}\end{array}\right.$,
∴△BPM≌△QPN(AAS),
∴BM=QN;
设BM=x,则NF=x,
∴PM=CM=CN=10+x,
∴CP=$\sqrt{2}$(10+x),
∵PM∥AB,
∴$\frac{CP}{AP}=\frac{CM}{BM}$,即$\frac{\sqrt{2}(10+x)}{4\sqrt{2}}=\frac{10+x}{x}$,
解得:x=4或x=-10(舍),
∴BM=4,CM=14,
∴BC=BM+CM=18,
∴正方形ABCD的面积为:18×18=324.
故答案为:324.
点评 本题考查了正方形的性质、直角三角形的性质、全等三角形的判定和全等三角形的性质以及平行线分线段成比例定理,解题的关键是作垂线段构造全等三角形.

练习册系列答案
相关题目
15.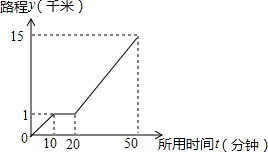 万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )
万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )
 万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )
万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )| A. | 小强家与小明家的路程为1千米 | |
| B. | 小强在小明家楼下的公共汽车站等10分钟 | |
| C. | 该公共汽车的平均速度为30 千米/小时 | |
| D. | 他们乘公共汽车用了30分钟 |
 如图,∠ABC=90°,P为射线BC上任意一点(点P和点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.补全图形,并求证:BF=EF.
如图,∠ABC=90°,P为射线BC上任意一点(点P和点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.补全图形,并求证:BF=EF.