题目内容
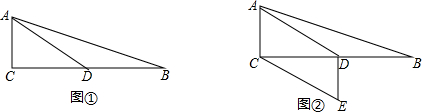
10.在△ABC中,∠ACB=90°,D是BC的中点,AC=2,AD=4.(Ⅰ)如图①,求CD,AB的长;
(Ⅱ)如图②,过点C作CE∥AD,过点D作DE⊥BC,DE与CE相交于点E,求点D到CE的距离.
分析 (Ⅰ)在Rt△ACD中,根据勾股定理可求CD,根据中点的定义可求BC,再在Rt△ACB中,根据勾股定理可求AB;
(Ⅱ)先根据平行四边形的判定得到四边形ACED是平行四边形,可求DE,CE,再根据三角形面积公式可求点D到CE的距离.
解答 解:(Ⅰ)在Rt△ACD中,CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∵D是BC的中点,
∴BC=2CD=4$\sqrt{3}$,
在Rt△ACB中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{13}$;
(Ⅱ)∵∠ACB=90°,DE⊥BC,
∴AC∥DE,
∵CE∥AD,
∴四边形ACED是平行四边形,
∴DE=AC=2,CE=AD=4,
∴点D到CE的距离为2$\sqrt{3}$×2÷2×2÷4=$\sqrt{3}$.
点评 此题考查了勾股定理,平行四边形的判定与性质,关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.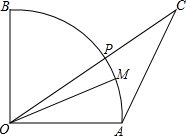 如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
 如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )| A. | 4 | B. | 2 | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
2. 二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.
二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.
(1)确定二次函数y1与直线AB的解析式y2;
(2)根据图象,分别确定当y1<y2,y1=y2时,自变量x的取值范围.
 二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.
二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.(1)确定二次函数y1与直线AB的解析式y2;
(2)根据图象,分别确定当y1<y2,y1=y2时,自变量x的取值范围.
20. 某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
表1 阅读课外书籍人数分组统计表
请你根据以上信息解答下列问题:
(1)这次共调查了学生多少人?
(2)E组人数在这次调查中所占的百分比是多少?
(3)求出表1中a的值,并补全图1;
(4)若该年级共有学生300人,请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人?
 某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.表1 阅读课外书籍人数分组统计表
| 分组 | 阅读课外书籍时间n(小时) | 人数 |
| A | 0≤n<3 | 3 |
| B | 3≤n<6 | 10 |
| C | 6≤n<9 | a |
| D | 9≤n<12 | 13 |
| E | 12≤n<15 | b |
| F | 15≤n<18 | c |
(1)这次共调查了学生多少人?
(2)E组人数在这次调查中所占的百分比是多少?
(3)求出表1中a的值,并补全图1;
(4)若该年级共有学生300人,请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人?
 如图,在△ABC中,BD=DC,∠1=∠2,
如图,在△ABC中,BD=DC,∠1=∠2, 如图是一座抛物形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降3m时,水面的宽为6$\sqrt{7}$m.
如图是一座抛物形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降3m时,水面的宽为6$\sqrt{7}$m.