题目内容
1.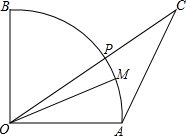 如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )| A. | 4 | B. | 2 | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
分析 由∠AOD的范围,求出AD的范围,在直角三角形ACD中,得出AC=2AD,即可求出a,b,进而得出结论.
解答 解:如图,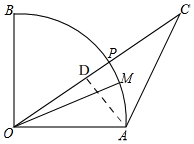
过点A作AD⊥OC于D,
∴∠ADC=∠ADO=90°,
在Rt△OAD中,OA=2,
∴sin∠AOD=$\frac{AD}{OA}$,
∴AD=OA•sin∠AOD=2sin∠AOD,
∵30°≤∠AOD≤90°,
∴$\frac{1}{2}$≤sin∠AOD≤1,
∴1≤2sin∠AOD≤2
即:1≤AD≤2,
在Rt△ADC中,∠ACO=30°,
∴AC=2AD,
∴2≤AC≤4,
∵线段AC的最大值为a,最小值为b,
∴a=4,b=2,
∴a-b=4-2=2;
故选B.
点评 此题主要考查了锐角三角函数的定义,含30°的直角三角形的性质;求出AD的范围是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,一副三角尺放在桌面上且它们的直角顶点重合在点O处,若∠AOD=150°,则∠BOD的度数为120°.
如图,一副三角尺放在桌面上且它们的直角顶点重合在点O处,若∠AOD=150°,则∠BOD的度数为120°.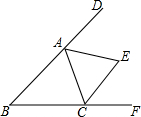 如图,△ABC中,∠B=30°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为75°.
如图,△ABC中,∠B=30°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为75°. 如图,每个小正方形的边长均为1,求图中阴影正方形的面积和边长.
如图,每个小正方形的边长均为1,求图中阴影正方形的面积和边长.