题目内容
2.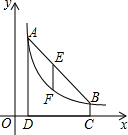 如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF=$\frac{1}{3}$AD,求出点E的坐标.
分析 (1)设反比例函数的解析式为y=$\frac{k}{x}$,根据题意得出方程组$\left\{\begin{array}{l}{6m=n}\\{m+5=n}\end{array}\right.$,求出方程组的解即可;
(2)设直线AB的解析式为y=ax+b,求出直线AB的解析式,设E点的横坐标为m,则E(m,-m+7),F(m,$\frac{6}{m}$),求出EF=-m+7-$\frac{6}{m}$,得出关于m的方程,求出m即可.
解答 解:(1)设反比例函数的解析式为y=$\frac{k}{x}$,
把(n,1)代入得:k=n,
即y=$\frac{n}{x}$,
∵点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5,
∴$\left\{\begin{array}{l}{6m=n}\\{m+5=n}\end{array}\right.$,
解得:m=1,n=6,
即A(1,6),B(6,1);
反比例函数的解析式为:y=$\frac{6}{x}$;
(2)设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入得:$\left\{\begin{array}{l}{a+b=6}\\{6a+b=1}\end{array}\right.$,
解得:a=-1,b=7,
即直线AB的解析式为:y=-x+7,
设E点的横坐标为m,则E(m,-m+7),F(m,$\frac{6}{m}$),
∴EF=-m+7-$\frac{6}{m}$,
∵EF=$\frac{1}{3}$AD,
∴-m+7-$\frac{6}{m}$=$\frac{1}{3}×6$,
解得:m=2,m2=3,
经检验都是原方程的解,
即E的坐标为(2,5)或(3,4).
点评 本题考查了用待定系数法求出反比例函数和一次函数的解析式,解二元一次方程组的应用,能得出二元一次方程组是解此题的关键,综合性比较强,比较好.

 阅读快车系列答案
阅读快车系列答案| A. | x=2 | B. | x=-2 | C. | x1=2,x2=-2 | D. | x=4 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 实数a在数轴上的位置如图所示,化简$\sqrt{(a-4)^{2}}$+$\sqrt{(a-11)^{2}}$.
实数a在数轴上的位置如图所示,化简$\sqrt{(a-4)^{2}}$+$\sqrt{(a-11)^{2}}$.