题目内容
6.已知等腰三角形的两边长分别是a和b,且满足|a-1|+(2a+3b-11)2=0,求这个等腰三角形的周长.分析 先根据非负数的性质求出a、b的值,再由三角形的三边关系判断出等腰三角形的腰与底边长,进而可得出结论.
解答 解:∵|a-1|+(2a+3b-11)2=0,
∴$\left\{\begin{array}{l}a-1=0\\ 2a+3b-11=0\end{array}\right.$,
解得$\left\{\begin{array}{l}a=1\\ b=3\end{array}\right.$.
∴当1为等腰三角形的腰时,不满足三角形的三边关系;
当3为等腰三角形的腰时,符合题意,此时三角形的周长=3+3+1=7.
点评 本题考查的是等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.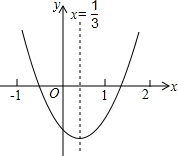 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
①c<0;②abc<0;③a-b+c>0;④2a-3b=0;⑤4a+2b+c>0.
你认为其中正确的是( )
 小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc<0;③a-b+c>0;④2a-3b=0;⑤4a+2b+c>0.
你认为其中正确的是( )
| A. | ①②④ | B. | ①③⑤ | C. | ②③⑤ | D. | ①③④⑤ |
14.如果α是锐角,且cosα=$\frac{4}{5}$,那么sinα的值( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 用一根长为10m的铝材制成如图所示的窗框,若窗框的面积为2m2,求窗框的高.
用一根长为10m的铝材制成如图所示的窗框,若窗框的面积为2m2,求窗框的高. 如图,D是△ABC的边AC上一点,过点D作DE∥AB交BC于点E.若∠DBE=∠BDE,试说明BD是△ABC的角平分线.
如图,D是△ABC的边AC上一点,过点D作DE∥AB交BC于点E.若∠DBE=∠BDE,试说明BD是△ABC的角平分线.