题目内容
7.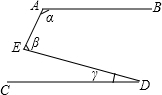 如图,AB∥CD,图中α、β、γ三个角之间的数量关系为( )
如图,AB∥CD,图中α、β、γ三个角之间的数量关系为( )| A. | α+β+γ=360° | B. | α+β-γ=180° | C. | α+β+γ=180° | D. | α-β-γ=90° |
分析 过E作EF∥AB,由平行线的性质可得EF∥CD,∠α+∠AEF=180°,∠FED=∠γ,由∠β=∠AEF+∠FED即可得∠α、∠β、∠γ之间的关系.
解答 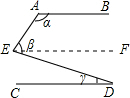 解:过点E作EF∥AB,
解:过点E作EF∥AB,
∴∠α+∠AEF=180°(两直线平行,同旁内角互补),
∵AB∥CD,
∴EF∥CD,
∴∠FED=∠EDC(两直线平行,内错角相等),
∵∠β=∠AEF+∠FED,
又∵∠γ=∠EDC,
∴∠α+∠β-∠γ=180°,
故选B.
点评 本题主要考查了平行线的性质,正确作出辅助线是解答此题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15.已知a2=25,$\sqrt{{b}^{2}}$=7,且|a+b|=a+b,则a-b的值为( )
| A. | 2或12 | B. | 2或-12 | C. | -2或12 | D. | -2或-12 |
16.在下列实数中,无理数是( )
| A. | 0 | B. | -$\frac{22}{7}$ | C. | $\sqrt{2}$ | D. | $\sqrt{9}$ |
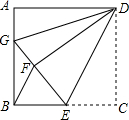 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=$\frac{72}{5}$.其中正确结论的个数是( )
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=$\frac{72}{5}$.其中正确结论的个数是( )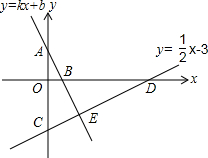 如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.
如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.