题目内容
11.不等式组$\left\{\begin{array}{l}{2x-1>0}\\{x+1≥0}\end{array}\right.$的解集是( )| A. | x$>\frac{1}{2}$ | B. | -1$≤x<\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x≥-1 |
分析 分别求出各不等式的解集,再求出其公共解集即可.
解答 解:$\left\{\begin{array}{l}2x-1>0①\\ x+1≥0②\end{array}\right.$,由①得,x>$\frac{1}{2}$,由②得,x≥-1,
故不等式组的解集为:x>$\frac{1}{2}$.
故选A.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.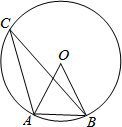 如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )
如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )
 如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )
如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )| A. | 64° | B. | 52° | C. | 54° | D. | 70° |
2.在下列调查中,适宜采用普查方式的是( )
| A. | 了解全国中学生的视力情况 | |
| B. | 了解九(1)班学生鞋子的尺码情况 | |
| C. | 检测一批电灯泡的使用寿命 | |
| D. | 调查郑州电视台《郑州大民生》栏目的收视率 |
19.在平面直角坐标系中,如果抛物线y=3x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系中抛物线的解析式是( )
| A. | y=3(x-2)2+2 | B. | y=3(x+2)2-2 | C. | y=3(x-2)2+2 | D. | y=3(x+2)2+2 |
16.用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
| A. | $\frac{25}{2}$mm | B. | $\frac{25}{2}$$\sqrt{3}$mm | C. | $\frac{25}{4}$mm | D. | $\frac{25}{4}$$\sqrt{3}$mm |

 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)
 小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)