题目内容
6.如图,在平面直角坐标系中,已知点A的坐标是(4,0),且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的表达式;
(2)在抛物线上是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.

分析 (1)先由已知条件求出B、C两点的坐标,再设抛物线的表达式是y=ax2+bx+c,将A,B,C三点的坐标代入,利用待定系数法即可求出抛物线的表达式;
(2)由(1)中所求解析式可设点P的坐标为(m,-m2+3m+4).当△ACP是以AC为直角边的直角三角形时,可分两种情况进行讨论:①以点A为直角顶点;②以点C为直角顶点;利用勾股定理分别列出关于m的方程,解方程即可.
解答 解:(1)∵点A的坐标是(4,0),
∴OA=4,
∵OA=OC=4OB,
∴OC=OA=4,OB=$\frac{1}{4}$OA=1,
∴点C的坐标是(0,4),点B的坐标是(-1,0).
设抛物线的表达式是y=ax2+bx+c,由题意得
$\left\{\begin{array}{l}{16a+4b+c=0}\\{a-b+c=0}\\{c=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\\{c=4}\end{array}\right.$,
∴抛物线的表达式是y=-x2+3x+4; (2)存在.
(2)存在.
设点P的坐标为(m,-m2+3m+4).
∵A(4,0),C(0,4),
∴AC2=42+42=32,AP2=(m-4)2+(-m2+3m+4)2,CP2=m2+(-m2+3m)2.
当△ACP是以AC为直角边的直角三角形时,可分两种情况:
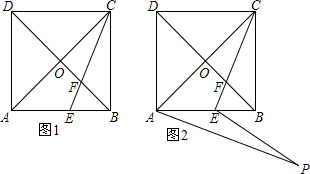
①如图1,如果点A为直角顶点,那么AC2+AP2=CP2,
即32+(m-4)2+(-m2+3m+4)2=m2+(-m2+3m)2,
整理得m2-2m-8=0,
解得m1=-2,m2=4(不合题意舍去),
则点P的坐标为(-2,-6);
②如图2,如果点C为直角顶点,那么AC2+CP2=AP2,
即32+m2+(-m2+3m)2=+(m-4)2+(-m2+3m+4)2,
整理得m2-2m=0,
解得m1=2,m2=0(不合题意舍去),
则点P的坐标为(2,6);
综上所述,所有符合条件的点P的坐标为(-2,-6)或(2,6).
点评 本题是二次函数的综合题,考查了利用待定系数法求抛物线的解析式,直角三角形的性质,二次函数图象上点的坐标特征,勾股定理的应用,一元二次方程的解法,完全平方公式等知识,难度适中.利用分类讨论与方程思想是解题的关键.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案| A. | 6π | B. | 4π | C. | 2π | D. | π |
| A. | x$>\frac{1}{2}$ | B. | -1$≤x<\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x≥-1 |
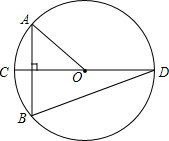 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
| A. | -a>-b | B. | -a+1>b+1 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ac<bc |
| A. | 平行四边形 | B. | 菱形 | C. | 正三角形 | D. | 正六边形 |

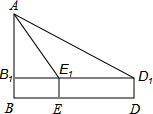 在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)
在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)