题目内容
1.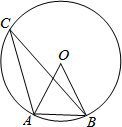 如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )
如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )| A. | 64° | B. | 52° | C. | 54° | D. | 70° |
分析 先根据圆周角定理求出∠AOB的度数,再由等腰三角形的性质即可得出结论.
解答 解:∵∠ACB=26°,
∴∠AOB=52°.
∵OA=OB,
∴∠ABO=$\frac{180°-52°}{2}$=64°.
故选A.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
7.下列关于矩形的说法中正确的是( )
| A. | 对角线相等的四边形是矩形 | B. | 矩形的对角线相等且互相平分 | ||
| C. | 对角线互相平分的四边形是矩形 | D. | 矩形的对角线互相垂直且平分 |
10.某校参加校园青春健身操比赛的16名运动员的身高如表:
则该校16名运动员身高的平均数和中位数分别是(单位:cm)( )
| 身高(cm) | 172 | 173 | 175 | 176 |
| 人数(个) | 4 | 4 | 4 | 4 |
| A. | 173cm,173cm | B. | 174cm,174cm | C. | 173cm,174cm | D. | 174cm,175cm |
11.不等式组$\left\{\begin{array}{l}{2x-1>0}\\{x+1≥0}\end{array}\right.$的解集是( )
| A. | x$>\frac{1}{2}$ | B. | -1$≤x<\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x≥-1 |
 小球在如图所示的地板上自由滚动,并随机停留在某块正方形的地砖上,则它停在白色地砖上的概率是$\frac{3}{5}$.
小球在如图所示的地板上自由滚动,并随机停留在某块正方形的地砖上,则它停在白色地砖上的概率是$\frac{3}{5}$.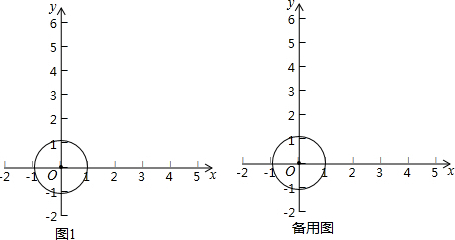
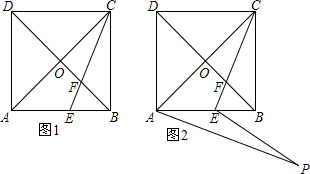
 如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$,
如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$, 如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).
如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).