Question

4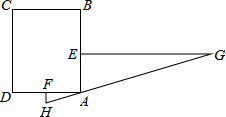．“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》．意思是说：如图，矩形城池ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB、AD中点，EG⊥AB，FH⊥AD，EG=15里，HG经过A点，则FH=（　　）

• A． 1.2 里
• B． 1.5 里
• C． 1.05 里
• D． 1.02 里

Answer 1

分析 首先根据题意得到△GEA∽△AFH，然后利用相似三角形的对应边的比相等列出比例式求得答案即可．

解答 解：如图所示：
∵EG⊥AB，FH⊥AD，HG经过A点，
∴FA∥EG，EA∥FH，
∴∠HFA=∠AEG=90°，∠FHA=∠EAG，
∴△GEA∽△AFH，
∴$\frac{EG}{FA}$=$\frac{EA}{FH}$．
∵AB=9里，DA=7里，EG=15里，
∴FA=3.5里，EA=4.5里，
∴$\frac{15}{3.5}$=$\frac{4.5}{FH}$，
解得：FH=1.05里．
故选：C．

点评 本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形．