题目内容
20.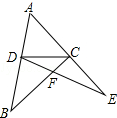 如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )| A. | 104° | B. | 118° | C. | 128° | D. | 136° |
分析 先根据等腰三角形的性质得出∠B=∠DCB,∠E=∠CDE,再利用三角形的内角和进行分析解答即可.
解答 解:∵BD=CD=CE,
∴∠B=∠DCB,∠E=∠CDE,
∵∠ADC+∠ACD=114°,
∴∠BDC+∠ECD=360°-104°=256°,
∴∠B+∠DCB+∠E+∠CDE=360°-256°=104°,
∴∠DCB+∠CDE=52°,
∴∠DFC=180°-52°=128°,
故选C.
点评 此题考查等腰三角形的性质,四边形的内角和,三角形的内角和,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
9.如果a2+3a+k分解后有一个因式为(a-1),那么k的值( )
| A. | 6 | B. | -6 | C. | -4 | D. | -5 |
 如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,那么每个直角三角形的周长为$5+\sqrt{13}$.
如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,那么每个直角三角形的周长为$5+\sqrt{13}$.