题目内容
15.甲口袋中装有3个相同的小球,它们分别写有数值-1,2,5;乙口袋中装有3个相同的小球,它们分别写有数值-4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y).(1)请用树状图或列表法表示点A的坐标的各种可能情况;
(2)求点A落在y=x2+x-4的概率.
分析 (1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;
(2)由(1)可求得(-1,-4),(2,2)在函数y=x2+x-4上,再利用概率公式即可求得答案.
解答 解:(1)列表如下:
甲 乙 | -4 | 2 | 3 |
| -1 | (-1,-4) | (-1,-2) | (-1,3) |
| 2 | (2,-4) | (2,2) | (2,3) |
| 5 | (5,-4) | (5,-2) | (5,3) |
(2)∵(-1,-4),(2,2)在函数y=x2+x-4上,
∴点A落在y=x2+x-4的概率P=$\frac{2}{9}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
5.下列各组线段中,不能作为直角三角形三边的是( )
| A. | 20,21,29 | B. | 9,12,15 | C. | 4,5,6 | D. | 15,8,17 |
3.如图所示的三个矩形中,其中相似形是( )


| A. | 甲与乙 | B. | 乙与丙 | C. | 甲与丙 | D. | 以上都不对 |
10.关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:
①2a+b<0;
②ab<0;
③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;
④抛物线y=2x2+ax+b-2的顶点在第四象限.
其中正确的结论有( )
①2a+b<0;
②ab<0;
③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;
④抛物线y=2x2+ax+b-2的顶点在第四象限.
其中正确的结论有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
20.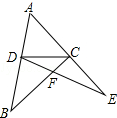 如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
 如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )| A. | 104° | B. | 118° | C. | 128° | D. | 136° |