题目内容
17.探究:22-21=2×21-1×21=2(1 )23-22=2×22-1×22=2(2 )
24-23=2×23-1×23=2(3 )
…
(1)请仔细观察,写出第4个等式;
(2)请你找规律,写出第n个等式;
(3)计算:20+21+22+…+22015+22016-22017.
分析 (1)根据幂的运算方法,可得21-20=2-1=1=20,22-21=4-2=2=21,23-22=8-4=4=22,据此解答即可;
(2)根据(1)中式子的规律,可得2n+1-2n=2n.
(3)设s=1+2+22+…+22016 ①,得2s=2+22+23+…+22017 ②,②-①得到s=22017-1,代入即可得.
解答 解:(1)探究:22-21=2×21-1×21=21;
23-22=2×22-1×22=22;
24-23=2×23-1×23=23;
…
∴25-24=2×24-1×24=24,
故答案为:1、2×22-1×22、2、2×23-1×23、3;
(2)由(1)知,第n个等式为:2n+1-2n=2×2n-1×2n=2n;
(3)设s=1+2+22+…+22016 ①,
∴2s=2+22+23+…+22017 ②,
由②-①:s=22017-1,
则原式=22017-1-22017=-1.
点评 此题主要考查了数字变化规律,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:2n+1-2n=2n成立.

练习册系列答案
相关题目
8. 如图,在矩形ABCD中,AB=6,AD=10,AD,AB,BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,且点为N,则DM的长为( )
如图,在矩形ABCD中,AB=6,AD=10,AD,AB,BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,且点为N,则DM的长为( )
 如图,在矩形ABCD中,AB=6,AD=10,AD,AB,BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,且点为N,则DM的长为( )
如图,在矩形ABCD中,AB=6,AD=10,AD,AB,BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,且点为N,则DM的长为( )| A. | $\frac{58}{7}$ | B. | 8 | C. | $\frac{40}{7}$ | D. | 2$\sqrt{13}$ |
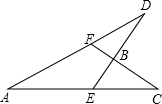 如图所示,已知∠A=27°,∠CBE=90°,∠C=30°,则∠D的度数为33度.
如图所示,已知∠A=27°,∠CBE=90°,∠C=30°,则∠D的度数为33度.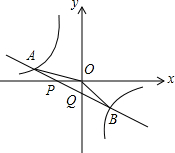 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m),B(1,n)两点,连接OA、OB,给出下列结论:①k1+k2>0;②n=-2m;③S△BOQ=-$\frac{1}{2}$b,则正确的是( )
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m),B(1,n)两点,连接OA、OB,给出下列结论:①k1+k2>0;②n=-2m;③S△BOQ=-$\frac{1}{2}$b,则正确的是( )
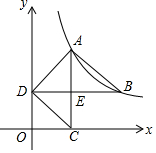 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.