题目内容
8. 如图,在矩形ABCD中,AB=6,AD=10,AD,AB,BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,且点为N,则DM的长为( )
如图,在矩形ABCD中,AB=6,AD=10,AD,AB,BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,且点为N,则DM的长为( )| A. | $\frac{58}{7}$ | B. | 8 | C. | $\frac{40}{7}$ | D. | 2$\sqrt{13}$ |
分析 连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=6,由于AD,AB,BC分别与⊙O相切于E,F,G三点,得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=7,由勾股定理列方程即可求出结果.
解答 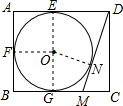 解:连接OE,OF,ON,OG,
解:连接OE,OF,ON,OG,
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=6,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=3,
∴DE=7,
∵DM是⊙O的切线,
∴DN=DE=7,MN=MG,
∴CM=10-3-MN=7-MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(7+NM)2=(7-NM)2+62,
∴NM=$\frac{9}{7}$,
∴DM=7+$\frac{9}{7}$=$\frac{58}{7}$.
故选A.
点评 本题考查了切线的性质,勾股定理,正方形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
16.下列二次分式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{12}$ | D. | $\sqrt{24}$ |
 如图,PA、PB是⊙O的两条切线,A、B是切点,PA=$\sqrt{3}$OA,阴影部分的面积为6π,则⊙O的半径长为3.
如图,PA、PB是⊙O的两条切线,A、B是切点,PA=$\sqrt{3}$OA,阴影部分的面积为6π,则⊙O的半径长为3.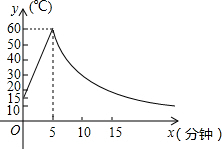 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.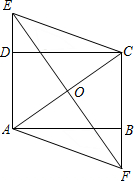 如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,连结AF、CE.
如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,连结AF、CE.