题目内容
7. 如图,下列条件中,能使△ACD∽△ABC的是( )
如图,下列条件中,能使△ACD∽△ABC的是( )| A. | $\frac{AC}{AD}$=$\frac{AB}{BC}$ | B. | $\frac{CD}{BC}$=$\frac{AD}{AC}$ | C. | CD2=AD•BD | D. | AC2=AD•AB |
分析 相似三角形的判定:
(1)三边法:三组对应边的比相等的两个三角形相似;
(2)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(3)两角法:有两组角对应相等的两个三角形相似.
由此结合各选项进行判断即可.
解答  解:A、$\frac{AC}{AD}$=$\frac{AB}{BC}$,不是对应边成比例,则不能使△ACD∽△ABC,故本选项错误;
解:A、$\frac{AC}{AD}$=$\frac{AB}{BC}$,不是对应边成比例,则不能使△ACD∽△ABC,故本选项错误;
B、只有$\frac{CD}{BC}$=$\frac{AD}{AC}$不能判定△ACD∽△ABC,故本选项错误;
C、由CD2=AD•BD得到:$\frac{CD}{AD}$=$\frac{BD}{CD}$,它不是对应边成比例,则不能使△ACD∽△ABC,故本选项错误;
D、由AC2=AD•AB得到:$\frac{AC}{AD}$=$\frac{AB}{AC}$,结合∠CAD=∠BAC可以判定△ACD∽△ABC,故本选项正确.
故选:D.
点评 本题考查了相似三角形的判定,解答本题的关键是熟练掌握相似三角形的判定定理,难度一般.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
17.小华和小刚兄弟两个同时从家去同一所学校上学,速度都是每分钟走50米.小华从家到学校走直线用了10分钟,而小刚从家出发先去找小明再到学校(均走直线),小刚到小明家用了6分钟,小明家到学校用了8分钟,小刚上学走了个( )
| A. | 锐角弯 | B. | 钝角弯 | C. | 直角弯 | D. | 不能确定 |
18.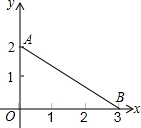 如图,线段AB对应的函数表达式为( )
如图,线段AB对应的函数表达式为( )
 如图,线段AB对应的函数表达式为( )
如图,线段AB对应的函数表达式为( )| A. | y=-$\frac{3}{2}$x+2 | B. | y=-$\frac{2}{3}$x+2 | C. | y=-$\frac{2}{3}$x+2(0≤x≤3) | D. | y=-$\frac{2}{3}$x+20(0<x<3) |
19.如图,下列四个几何体中,俯视图不同与其他几何体的是( )


| A. | ④ | B. | ③ | C. | ② | D. | ① |
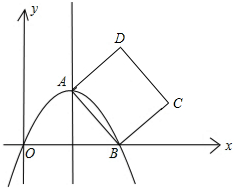 如图,抛物线y=ax2+bx+c的顶点为A(4,4),且抛物线经过原点,和x轴相交于另一点B,以AB为一边在直线AB的右侧画正方形ABCD.
如图,抛物线y=ax2+bx+c的顶点为A(4,4),且抛物线经过原点,和x轴相交于另一点B,以AB为一边在直线AB的右侧画正方形ABCD. 建立直角坐标系,描出下列各点A(-2,2),B(-1,0),C(0,2)
建立直角坐标系,描出下列各点A(-2,2),B(-1,0),C(0,2)