题目内容
12.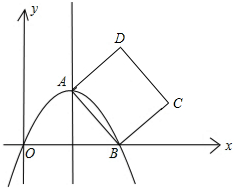 如图,抛物线y=ax2+bx+c的顶点为A(4,4),且抛物线经过原点,和x轴相交于另一点B,以AB为一边在直线AB的右侧画正方形ABCD.
如图,抛物线y=ax2+bx+c的顶点为A(4,4),且抛物线经过原点,和x轴相交于另一点B,以AB为一边在直线AB的右侧画正方形ABCD.(1)求抛物线的解析式;
(2)点C、D的坐标分别是(12,4)和(8,8);
(3)能否将此抛物线沿着直线x=4平移,使平移后的抛物线恰好经过正方形ABCD的另两个顶点C、D?若能,写出平移后抛物线的解析式;若不能,请说明理由.
分析 (1)可用顶点式二次函数通式来设抛物线的解析式,将原点坐标代入即可求出其解析式.
(2)根据抛物线的顶点A的坐标即可得出抛物线的对称轴为x=4,已知O、B关于抛物线的对称轴对称,那么B点的坐标为(8,0).根据A(4,4)可得出∠AOB=45°,即△OAB为等腰直角三角形,因此O、A、D三点同线,直线BD与y轴平行,直线AC与x轴平行,因此D点坐标为(8,8),C点坐标为(12,4);
(3)可先设出平移后抛物线的解析式,然后将D点坐标代入,即可求出平移后抛物线的解析式,再将C点坐标代入抛物线中进行验证即可;
解答 解:(1)设抛物线的解析式为y=a(x-4)2+4,
则有:a(0-4)2+4=0,
解得:a=-$\frac{1}{4}$.
∴y=-$\frac{1}{4}$(x-4)2+4;
(2)根据A(4,4)可知,∠AOB=45° ,
,
∵AO=AB,
∴△AOB为等腰直角三角形.
∴∠OAB=90°,即O、A、D三点共线,
因此直线BD∥y轴,直线AC∥x轴,
则有:C(12,4),D(8,8).
(3)设平移后的抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4+h(h>0),
将C点坐标代入有:4=-$\frac{1}{4}$(12-4)2+4+h,
解得h=16
∴平移后抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+20
当x=8时,y=12≠8,
因此不能使平移后的抛物线恰好经过正方形ABCD的另两个顶点C、D.
点评 此题主要考查了二次函数的平移以及等腰直角三角形和正方形的性质等知识,正确利用二次函数图象上点的坐标性质得出是解题关键.

练习册系列答案
相关题目
7. 如图,下列条件中,能使△ACD∽△ABC的是( )
如图,下列条件中,能使△ACD∽△ABC的是( )
 如图,下列条件中,能使△ACD∽△ABC的是( )
如图,下列条件中,能使△ACD∽△ABC的是( )| A. | $\frac{AC}{AD}$=$\frac{AB}{BC}$ | B. | $\frac{CD}{BC}$=$\frac{AD}{AC}$ | C. | CD2=AD•BD | D. | AC2=AD•AB |
17.若$\sqrt{\frac{x-2}{3-x}}$=$\frac{\sqrt{x-2}}{\sqrt{3-x}}$成立,则x的取值范围为( )
| A. | x≥2 | B. | x≤3 | C. | 2≤x≤3 | D. | 2≤x<3 |
2. 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2018的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2018的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2018的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2018的纵坐标为( )| A. | 0 | B. | -3×$(\frac{3\sqrt{3}}{2})^{2017}$ | C. | $(2\sqrt{3})^{2018}$ | D. | 3×$(\frac{2\sqrt{3}}{3})^{2017}$ |
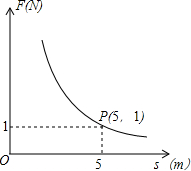 在对物体做功一定情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,则当力达到10N时,物体在力的方向上移动的距离是0.5m.
在对物体做功一定情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,则当力达到10N时,物体在力的方向上移动的距离是0.5m. 某博物馆通过浮动门票价格的方法既保证必要的收入,又要尽量控制参观人数,调查统计发现,每周参观人数与票价之间的关系可近似的看成如图所示的一次函数关系.如果门票价格定为6元,那么本周大约有9000人参观.
某博物馆通过浮动门票价格的方法既保证必要的收入,又要尽量控制参观人数,调查统计发现,每周参观人数与票价之间的关系可近似的看成如图所示的一次函数关系.如果门票价格定为6元,那么本周大约有9000人参观.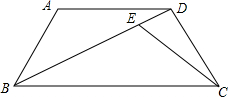 如图.梯形ABCD中.AD∥BC,AB=CD=2,AD=4,BC=6,点E在BD上,且∠DCE=∠ADB.
如图.梯形ABCD中.AD∥BC,AB=CD=2,AD=4,BC=6,点E在BD上,且∠DCE=∠ADB.