题目内容
在梯形ABCD中,DC∥AB,AD=2
,上底DC=2m,BC=2m,∠DAB=30°,∠CBA=60°,求下底AB的长.
| 3 |
考点:梯形
专题:
分析:过C作CE∥AD交AB于E,则四边形ADCE是平行四边形,再证明三角形BEC为直角三角形即可求出AB的长.
解答: 解:如图,过C作CE∥AD交AB于E,
解:如图,过C作CE∥AD交AB于E,
∵AB∥DC,
∴四边形ADCE是平行四边形,
∵DC=AE=2cm,
∵∠DAB=30°,
∴∠CEB=30°,
∵∠CBA=60°,
∴∠ECB=90°
∴△CEB是直角三角形,
∴BE=2BC=4cm,
∴AB=AE+EB=2+4=6cm.
 解:如图,过C作CE∥AD交AB于E,
解:如图,过C作CE∥AD交AB于E,∵AB∥DC,
∴四边形ADCE是平行四边形,
∵DC=AE=2cm,
∵∠DAB=30°,
∴∠CEB=30°,
∵∠CBA=60°,
∴∠ECB=90°
∴△CEB是直角三角形,
∴BE=2BC=4cm,
∴AB=AE+EB=2+4=6cm.
点评:此题考查等腰梯形的性质、平行四边形的判定和性质以及直角三角形的判定及性质.

练习册系列答案
相关题目
一家商店一月份把某种进货价为100元的商品,提高60%出售,到三月份再声称以8折(80%)大拍卖,那么该商品三月份的价格比进货价( )
| A、高12.8%元 |
| B、低12.8%元 |
| C、高40元 |
| D、高28元 |
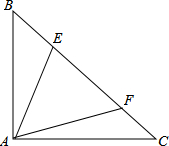 如图,在Rt△ABC中,∠BAC=90°,AB=AC,E、F分别是BC上两点,满足∠EAF=45°,若AB=
如图,在Rt△ABC中,∠BAC=90°,AB=AC,E、F分别是BC上两点,满足∠EAF=45°,若AB= 如图,在⊙O中,
如图,在⊙O中,