题目内容
已知a、b、c≠0，且
+
+
+
的最大值为m，最小值为n，则2013（m+n+1）= ．
| a |
| |a| |
| b |
| |b| |
| c |
| |c| |
| abc |
| |abc| |
考点：绝对值
专题：
分析：分别利用①a，b，c都大于0，②a，b，c都小于0，③a，b，c，一负两正，④a，b，c，一正两负进而分析得出即可．
解答：解：∵a，b，c都不等于0，
∴有以下情况：
①a，b，c都大于0，原式=1+1+1+1=4；
②a，b，c都小于0，原式=-1-1-1-1=-4；
③a，b，c，一负两正，不妨设a＜0，b＞0，c＞0，
原式=-1+1+1-1=0；
④a，b，c，一正两负，不妨设a＞0，b＜0，c＜0，
原式=-1-1-1+1=-2；
∴m=4，n=-4，
∴2013m+n+1=20134-4+1=2013．
故答案为：2013．
∴有以下情况：
①a，b，c都大于0，原式=1+1+1+1=4；
②a，b，c都小于0，原式=-1-1-1-1=-4；
③a，b，c，一负两正，不妨设a＜0，b＞0，c＞0，
原式=-1+1+1-1=0；
④a，b，c，一正两负，不妨设a＞0，b＜0，c＜0，
原式=-1-1-1+1=-2；
∴m=4，n=-4，
∴2013m+n+1=20134-4+1=2013．
故答案为：2013．
点评：此题主要考查了绝对值的性质，利用分类讨论得出是解题关键．
练习册系列答案
相关题目
在△ABC中，∠ACB=90°，CE⊥AB于点E，D在AB延长线上，且∠DCB=∠A，BD：CD=1：2，AE=
如图，将矩形ABCD绕点A顺时针旋转90°后，得到矩形AB′C′D′，如果CD=3DA=3，那么CC′=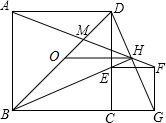
如图，ABCD、CEFG是正方形，E在CD上，且BE平分∠DBC，O是BD中点，直线BE、DG交于H．BD，AH交于M，连接OH，则OH=
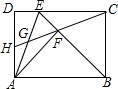如图，在矩形ABCD，AB=