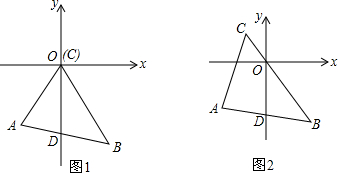题目内容
 如图,已知扇形AOB的半径为6,∠AOB=90°,等边△CDE的顶点C、D、E分别在OA、OB、
如图,已知扇形AOB的半径为6,∠AOB=90°,等边△CDE的顶点C、D、E分别在OA、OB、 |
| AB |
考点:圆的综合题
专题:
分析:取CD的中点G,连接GO,EG,OE.根据正三角形外心的性质和相似三角形的性质解答即可.
解答: 解:如图,取CD的中点G,连接GO,EG,OE.
解:如图,取CD的中点G,连接GO,EG,OE.
可得GO=CG=GD=
DC,
∵P为正△DEC的外心,
∴G,E,P三点共线,PE=2GP,
∴GE=3GP,GC=
GP,
∴
=
=
,
=
=
,
∴
=
,
∵∠PGO=∠OGE,
∴△PGO∽△OGE,
∴
=
=
,
∴OP=
OE=
×6=2
.
故答案为2
.
 解:如图,取CD的中点G,连接GO,EG,OE.
解:如图,取CD的中点G,连接GO,EG,OE.可得GO=CG=GD=
| 1 |
| 2 |
∵P为正△DEC的外心,
∴G,E,P三点共线,PE=2GP,
∴GE=3GP,GC=
| 3 |
∴
| GO |
| GP |
| ||
| GP |
| 3 |
| GE |
| GO |
| 3GP | ||
|
| 3 |
∴
| GO |
| GP |
| GE |
| GO |
∵∠PGO=∠OGE,
∴△PGO∽△OGE,
∴
| PO |
| OE |
| PG |
| GO |
| ||
| 3 |
∴OP=
| ||
| 3 |
| ||
| 3 |
| 3 |
故答案为2
| 3 |
点评:本题考查了圆的相关内容,要充分利用圆、相似三角形、三角形的外心的性质解答.

练习册系列答案
相关题目
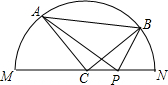 如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若
如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若 |
| MA |
 |
| BN |
| A、10° | B、15° |
| C、20° | D、25° |
泗水县龙城中学去年对实验器材的投资为2万元,预计明年的投资为8万元.若设该校今明两年在实验器材投资上年平均增长率是x,根据题意,下面所列方程正确的是( )
| A、2(1+x)2=8 |
| B、8(1+x)2=2 |
| C、2(1-x)2=8 |
| D、2+2(1+x)+2(1+x)2=8 |
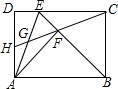 如图,在矩形ABCD,AB=
如图,在矩形ABCD,AB=