题目内容
1×1!+2×2!+3×3!+…+2011×2011!mod2012的值为( )(mod为取余,如27mod5=2)
| A、1 | B、3 |
| C、1006 | D、2011 |
考点:带余除法
专题:
分析:将1×1!+2×2!+3×3!+…+2011×2011!变形为2×1!+2×2!+3×3!+…+2011×2011!-1×1!,从而得到2012!-1,依此即可得到这个数对2012取余数的结果为2011.
解答:解:1×1!+2×2!+3×3!+…+2011×2011!
=2×1!+2×2!+3×3!+…+2011×2011!-1×1!
=2!+2×2!+3×3!+…+2011×2011!-1
=3×2!+3×3!+…+2011×2011!-1
=3!+3×3!+…+2011×2011!-1
=…
=2012!-1
显然,这个数对2012取余数的结果为2011.
故选D.
=2×1!+2×2!+3×3!+…+2011×2011!-1×1!
=2!+2×2!+3×3!+…+2011×2011!-1
=3×2!+3×3!+…+2011×2011!-1
=3!+3×3!+…+2011×2011!-1
=…
=2012!-1
显然,这个数对2012取余数的结果为2011.
故选D.
点评:考查了带余除法,解题的关键是将式子变形得到结果为得到2012!-1,依此即可求解.

练习册系列答案
相关题目
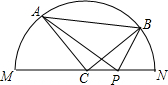 如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若
如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若 |
| MA |
 |
| BN |
| A、10° | B、15° |
| C、20° | D、25° |
某运动员投一次篮投中的概率为0.8,则下列说法正确的是( )
| A、该运动员投10次篮,必有8次投中 |
| B、该运动员投10次篮,恰好8次投中的可能性很大 |
| C、该运动员投1000次篮,约有800次投中 |
| D、该运动员投1000次篮,必有800次投中 |
泗水县龙城中学去年对实验器材的投资为2万元,预计明年的投资为8万元.若设该校今明两年在实验器材投资上年平均增长率是x,根据题意,下面所列方程正确的是( )
| A、2(1+x)2=8 |
| B、8(1+x)2=2 |
| C、2(1-x)2=8 |
| D、2+2(1+x)+2(1+x)2=8 |
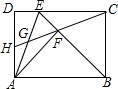 如图,在矩形ABCD,AB=
如图,在矩形ABCD,AB=