题目内容
 如图,△ADE为等边三角形,向两方延长DE,使得BD=DE=EC.连接AB、AC得△ABC,则∠BAC=
如图,△ADE为等边三角形,向两方延长DE,使得BD=DE=EC.连接AB、AC得△ABC,则∠BAC=考点:等边三角形的性质,等腰三角形的性质
专题:
分析:先根据等边三角形的性质得出AD=DE=AE,∠DAE=∠ADE=∠AED=60°,再根据BD=DE=EC得出AD=BD,AE=CE,由等腰三角形的性质求出∠DAB与∠EAC的度数,进而可得出结论.
解答:解:∵△ADE为等边三角形,
∴AD=DE=AE,∠DAE=∠ADE=∠AED=60°,
∵BD=DE=EC,
∴AD=BD,AE=CE,
∴∠DAB=∠EAC=
=30°.
∴∠BAC=∠BAD+∠DAE+∠CAE=30°+60°+30°=120°.
故答案为:120°.
∴AD=DE=AE,∠DAE=∠ADE=∠AED=60°,
∵BD=DE=EC,
∴AD=BD,AE=CE,
∴∠DAB=∠EAC=
| 180°-120° |
| 2 |
∴∠BAC=∠BAD+∠DAE+∠CAE=30°+60°+30°=120°.
故答案为:120°.
点评:本题考查的是等边三角形的性质,熟知等边三角形的三个内角都相等,且都等于60°是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠BAC=90,BC∥x轴,抛物线y=ax2-2ax+3经过△ABC的三个顶点,并且与x轴交于点D、E,点A为抛物线的顶点.
如图,在△ABC中,∠BAC=90,BC∥x轴,抛物线y=ax2-2ax+3经过△ABC的三个顶点,并且与x轴交于点D、E,点A为抛物线的顶点. 如图,在?ABCD中,AC=6,BD=8,AC⊥BD,则AB的长为
如图,在?ABCD中,AC=6,BD=8,AC⊥BD,则AB的长为 如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=2cm,BD=4cm,则BC=
如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=2cm,BD=4cm,则BC= 如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:
如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论: 如图在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第200次跳动至点A200的坐标是
如图在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第200次跳动至点A200的坐标是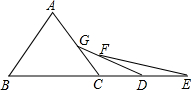 如图,已知△ABC中AB=AC,∠A=68°,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=
如图,已知△ABC中AB=AC,∠A=68°,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=