题目内容
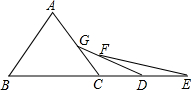如图，已知△ABC中AB=AC，∠A=68°，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=考点：等腰三角形的性质
专题：
分析：由于△ABC是等腰三角形，顶角∠A=68°，那么∠B=∠1=56°，而CD=CG，那么∠CGD=∠2，而∠1是△CDG的外角，可得∠1=2∠2，同理有∠2=2∠E，等量代换有4∠E=56°，解即可求∠E．
解答：
解：如图，
∵△ABC中AB=AC，∠A=68°，
∴∠B=∠1=56°，
∵CD=CG，
∴∠CGD=∠2，
∴∠1=2∠2，
同理有∠2=2∠E，
∴4∠E=56°，
∴∠E=14°．
故答案为14．
解：如图，∵△ABC中AB=AC，∠A=68°，
∴∠B=∠1=56°，
∵CD=CG，
∴∠CGD=∠2，
∴∠1=2∠2，
同理有∠2=2∠E，
∴4∠E=56°，
∴∠E=14°．
故答案为14．
点评：本题考查了等腰三角形的性质、三角形内角和定理及外角的性质，解题的关键是利用外角性质得出∠1=2∠2，∠2=2∠E．
练习册系列答案
相关题目
如图，△ADE为等边三角形，向两方延长DE，使得BD=DE=EC．连接AB、AC得△ABC，则∠BAC=
如图，一条公路修到湖边时，需拐弯绕湖而过；如果第一次拐的角∠A=96°，第二次拐的角∠B=136°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C=