Question

7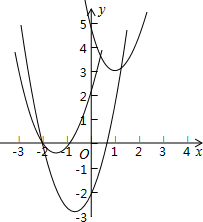．在平面直角坐标系中，点O为坐标原点，抛物线y=ax²+bx+5经过点M（1，3）和N（3，5）
（1）试判断该抛物线与x轴交点的情况；
（2）平移这条抛物线，使平移后的抛物线经过点A（-2，0），且与y轴交于点B，同时满足以A、O、B为顶点的三角形是等腰直角三角形，请你写出平移过程，并说明理由．

Answer 1

分析 （1）把M、N两点的坐标代入抛物线解析式可求得a、b的值，可求得抛物线解析式，再根据一元二次方程根的判别式，可判断抛物线与x轴的交点情况；
（2）利用A点坐标和等腰三角形的性质可求得B点坐标，设出平移后的抛物线的解析式，把A、B的坐标代入可求得平移后的抛物线的解析式，比较平移前后抛物线的顶点的变化即可得到平移的过程．

解答 解：
（1）由抛物线过M、N两点，
把M、N坐标代入抛物线解析式可得$\left\{\begin{array}{l}{a+b+5=3}\\{9a+3b+5=5}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=1}\\{b=-3}\end{array}\right.$，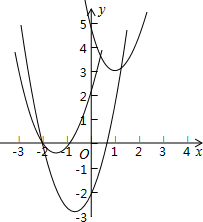
∴抛物线解析式为y=x²-3x+5，
令y=0可得x²-3x+5=0，
该方程的判别式为△=（-3）²-4×1×5=9-20=-11＜0，
∴抛物线与x轴没有交点；
（2）∵△AOB是等腰直角三角形，A（-2，0），点B在y轴上，
∴B点坐标为（0，2）或（0，-2），
可设平移后的抛物线解析式为y=x²+mx+n，
①当抛物线过点A（-2，0），B（0，2）时，代入可得$\left\{\begin{array}{l}{n=2}\\{4-2m+n=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{m=3}\\{n=2}\end{array}\right.$，
∴平移后的抛物线为y=x²+3x+2，
∴该抛物线的顶点坐标为（-$\frac{3}{2}$，-$\frac{1}{4}$），而原抛物线顶点坐标为（$\frac{3}{2}$，$\frac{11}{4}$），
∴将原抛物线先向左平移3个单位，再向下平移3个单位即可获得符合条件的抛物线；
②当抛物线过A（-2，0），B（0，-2）时，代入可得$\left\{\begin{array}{l}{n=-2}\\{4-2m+n=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{m=1}\\{n=-2}\end{array}\right.$，
∴平移后的抛物线为y=x²+x-2，
∴该抛物线的顶点坐标为（-$\frac{1}{2}$，-$\frac{9}{4}$），而原抛物线顶点坐标为（$\frac{3}{2}$，$\frac{11}{4}$），
∴将原抛物线先向左平移2个单位，再向下平移5个单位即可获得符合条件的抛物线．

点评 本题为二次函数的综合应用，涉及知识点有待定系数法、函数与方程的关系、等腰三角形的性质、坐标平移和分类讨论等．在（1）中注意方程与函数的关系，在（2）中确定出B点的坐标是解题的关键，注意抛物线顶点坐标的求法．本题属于基础题，难度不大．