题目内容
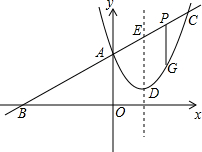 如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足sin∠ABO=
如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足sin∠ABO=
| ||
| 5 |
(1)求k,m和这个二次函数的解析式;
(2)点E是直线BC与抛物线对称轴的交点,当△PGE∽△AOB时,求点P的坐标;
(3)若PG=
| 21 |
| 16 |
考点:二次函数综合题
专题:
分析:(1)根据抛物线的顶点设抛物线的解析式为y=a(x-1)2+1,把A的坐标代入即可求得a,进而求得抛物线的解析式,根据sin∠ABO=
,求得B的坐标,然后根据待定系数法即可求得k,m;
(2)先求得直线AB的解析式,设P(x,
x+2),然后求得E的坐标,根据△PGE∽△AOB对应边成比例求得P的横坐标,进而求得纵坐标;
(3)分两种情况讨论求得;
| ||
| 5 |
(2)先求得直线AB的解析式,设P(x,
| 1 |
| 2 |
(3)分两种情况讨论求得;
解答:解:(1)∵二次函数图象的顶点坐标为D(1,1),
∴设y=a(x-1)2+1,
∵A(0,2),
∴2=a+1,解得,a=1,
∴二次函数的解析式为:y=x2-2x+2,
∵A(0,2),sin∠ABO=
,
∴AB=2
,
∴BO=4,
∴B(-4,0),
代入y=kx+m得
解得
(2)由(1)知
∴y=
x+2,
∵点E是直线BC与抛物线对称轴的交点,抛物线对称轴是x=1,
y=
+2=
,
∴点E(1,
),
∵△PGE∽△AOB,
∴∠PGE=90°,
设P(x,
x+2),
∴PG=
x+2-(x2-2x+2)=-x2+
x,EG=x-1
∵AO=2,BO=4,
∴
=
∴
=
,
解得:x=1+
,或x=1-
(舍去),
∴P(1+
,
);
(3)设P(x,
x+2),
当F在直线的下方时,PG=
x+2-(x2-2x+2)=-x2+
x,
所以-x2+
x=
,解得x1=
,x2=
,
把x1=
,x2=
,代入y=x2-2x+2,解得y1=
,y2=
,
所以F(
,
)或(
,
);
当F在直线的上方时,PG=x2-2x+2-(
x+2)=x2-
x,
所以x2-
x=
,解得:x3=
,x4=
,
把x3=
,x4=
代入y=x2-2x+2,解得:y3=
,y4=
;
所以F(
,
)或(
,
)
∴设y=a(x-1)2+1,
∵A(0,2),
∴2=a+1,解得,a=1,
∴二次函数的解析式为:y=x2-2x+2,
∵A(0,2),sin∠ABO=
| ||
| 5 |
∴AB=2
| 5 |
∴BO=4,
∴B(-4,0),
代入y=kx+m得
|
|
(2)由(1)知
|
∴y=
| 1 |
| 2 |
∵点E是直线BC与抛物线对称轴的交点,抛物线对称轴是x=1,
y=
| 1 |
| 2 |
| 5 |
| 2 |
∴点E(1,
| 5 |
| 2 |
∵△PGE∽△AOB,
∴∠PGE=90°,
设P(x,
| 1 |
| 2 |
∴PG=
| 1 |
| 2 |
| 5 |
| 2 |
∵AO=2,BO=4,
∴
| AO |
| PG |
| BO |
| EG |
∴
| 2 | ||
-x2+
|
| 4 |
| x-1 |
解得:x=1+
| ||
| 2 |
| ||
| 2 |
∴P(1+
| ||
| 2 |
10+
| ||
| 4 |
(3)设P(x,
| 1 |
| 2 |
当F在直线的下方时,PG=
| 1 |
| 2 |
| 5 |
| 2 |
所以-x2+
| 5 |
| 2 |
| 21 |
| 16 |
| 3 |
| 4 |
| 7 |
| 4 |
把x1=
| 3 |
| 4 |
| 7 |
| 4 |
| 17 |
| 16 |
| 25 |
| 16 |
所以F(
| 3 |
| 4 |
| 17 |
| 16 |
| 7 |
| 4 |
| 25 |
| 16 |
当F在直线的上方时,PG=x2-2x+2-(
| 1 |
| 2 |
| 5 |
| 2 |
所以x2-
| 5 |
| 2 |
| 21 |
| 16 |
5+
| ||
| 4 |
5-
| ||
| 4 |
把x3=
5+
| ||
| 4 |
5-
| ||
| 4 |
63+2
| ||
| 16 |
63-2
| ||
| 16 |
所以F(
5+
| ||
| 4 |
63+2
| ||
| 16 |
5-
| ||
| 4 |
63-2
| ||
| 16 |
点评:本题考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,三角形相似的性质,三角形的面积,方程思想的应用,综合性较强,有一定的难度.

练习册系列答案
相关题目
 如图,在△ABC中,D,E,F,分别是AB,BC,AC的中点,求证:四边形BEFD是平行四边形.
如图,在△ABC中,D,E,F,分别是AB,BC,AC的中点,求证:四边形BEFD是平行四边形.
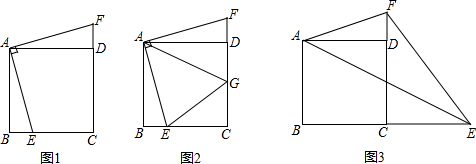
 如图,在梯形ABCD中,AD∥BC,∠DCB=60°,BD⊥CD,BC=6,AD=2.求AB长.
如图,在梯形ABCD中,AD∥BC,∠DCB=60°,BD⊥CD,BC=6,AD=2.求AB长. 如图,已知BE平分∠ABC,DE∥BC,AD=3,DE=2,AC=10,则AE的长度是
如图,已知BE平分∠ABC,DE∥BC,AD=3,DE=2,AC=10,则AE的长度是