题目内容
 如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点P.
如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点P.(1)求证:BE是⊙O的切线;
(2)若CP=2,PF=8,求AC的长;
(3)过点D作DG∥BE交EF于点G,过G作GH∥DE交DF于点H,则易知△DHG是等边三角形;设等边△ABC、△BDC、△DHG的面积分别为S1、S2、S3,试探究S1、S2、S3之间的数量关系,并说明理由.
考点:圆的综合题
专题:
分析:(1)连接OB,只要证明∠OBE=90°即可求解;
(2)连接PB,易证∠CPB=∠CBF,则可以得到△CPB∽△CBF,根据相似三角形对应边的比相等即可得证;
(3)作出DG与GH,易证AC∥BE∥DG,BC∥DE∥HG,根据平行线分线段成比例定理即可得证.
(2)连接PB,易证∠CPB=∠CBF,则可以得到△CPB∽△CBF,根据相似三角形对应边的比相等即可得证;
(3)作出DG与GH,易证AC∥BE∥DG,BC∥DE∥HG,根据平行线分线段成比例定理即可得证.
解答: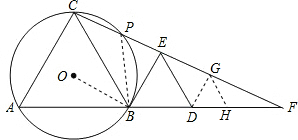 (1)证明:连接OB,由题意得,
(1)证明:连接OB,由题意得,
∠ABC=∠EBD=60°,
∴∠OBC=30°∠CBE=60°,
则∠OBE=90°,
∴BE是⊙O的切线;
(2)解:连接PB,
∵∠A=∠60°
∴∠CPB=120°,
∵∠CBF=120°,
∴∠CPB=∠CBF,
∵∠BCF=∠BCP,
∴△CPB∽△CBF,
∴
=
即CB2=CP•CF
∵AC=CB
∴AC2=CP•CF,
∵CP=2,PF=8,
∴AC=
=4
;
(3)解:根据题意,作出DG与GH,
由题意可得:AC∥BE∥DG,BC∥DE∥HG
∴
=
=
∵
=(
)2
=(
)2
∴
=
,即S22=S1•S3
∴所求的数量关系是S22=S1•S3.
 (1)证明:连接OB,由题意得,
(1)证明:连接OB,由题意得,∠ABC=∠EBD=60°,
∴∠OBC=30°∠CBE=60°,
则∠OBE=90°,
∴BE是⊙O的切线;
(2)解:连接PB,
∵∠A=∠60°
∴∠CPB=120°,
∵∠CBF=120°,
∴∠CPB=∠CBF,
∵∠BCF=∠BCP,
∴△CPB∽△CBF,
∴
| CP |
| CB |
| CB |
| CF |
∵AC=CB
∴AC2=CP•CF,
∵CP=2,PF=8,
∴AC=
| 80 |
| 5 |
(3)解:根据题意,作出DG与GH,
由题意可得:AC∥BE∥DG,BC∥DE∥HG
∴
| AB |
| BD |
| CE |
| EG |
| BD |
| DH |
∵
| S1 |
| S2 |
| AB |
| BD |
| S2 |
| S3 |
| BD |
| DH |
∴
| S1 |
| S2 |
| S2 |
| S3 |
∴所求的数量关系是S22=S1•S3.
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目