题目内容
10.在平面直角坐标系中,把抛物线y=$\frac{1}{2}{x}^{2}$+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是y=$\frac{1}{2}$(x+1)2+4.分析 先求出原抛物线的顶点坐标,再根据向左平移横坐标减,向上平移纵坐标加求出平移后的抛物线的顶点坐标,然后写出抛物线解析式即可.
解答 解:∵抛物线y=$\frac{1}{2}$x2+1的顶点坐标为(0,1),
∴向上平移3个单位,再向左平移1个单位后的抛物线的顶点坐标为(-1,4),
∴所得抛物线的解析式为y=$\frac{1}{2}$(x+1)2+4.
故答案为y=$\frac{1}{2}$(x+1)2+4.
点评 本题主要考查的了二次函数图象与几何变换,利用顶点坐标的平移确定函数图象的平移可以使求解更简便,平移规律“左加右减,上加下减”.

练习册系列答案
相关题目
15.生活中我们经常用的梯子,已知长度不变的梯子根地面所成的锐角为α,下面关于α的三角函数与梯子的倾斜程度之间,叙述正确的是( )
| A. | sinα的值越大,梯子越陡 | B. | cosα的值越大,梯子越陡 | ||
| C. | tanα的值越小,梯子越陡 | D. | 陡缓程度与α的函数值无关 |
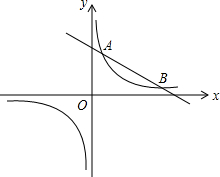 如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.
如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.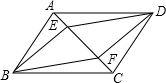 已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在AC上,且AF=CE.求证:四边形BEDF是平行四边形.
已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在AC上,且AF=CE.求证:四边形BEDF是平行四边形.