题目内容
已知矩形纸片ABCD中,AB=24厘米,BC=10厘米.
(1)按如下操作:先将矩形纸片上下对折,而后左右对折,再沿对角线对折,而后展开得到图中的折痕四边形EFGH(如图1),求菱形EFGH的面积.
(2)如图2,将矩形纸片ABCD先沿对角线AC对折,再将纸片折叠使点A与点C重合得折痕EF,则四边形AECF必为菱形,请加以证明.
(3)请通过一定的操作,构造一个菱形EFGH(不同于第(1)题中的特殊图形),使菱形的四个顶点分别落在矩形ABCD的四条边上(E、F、G、H分别在边AB、BC、CD、DA上,且不与矩形ABCD的顶点重合).
①请简述操作的方法,并在图3中画出菱形EFGH.
②求菱形EFGH的面积的取值范围.

(1)按如下操作:先将矩形纸片上下对折,而后左右对折,再沿对角线对折,而后展开得到图中的折痕四边形EFGH(如图1),求菱形EFGH的面积.
(2)如图2,将矩形纸片ABCD先沿对角线AC对折,再将纸片折叠使点A与点C重合得折痕EF,则四边形AECF必为菱形,请加以证明.
(3)请通过一定的操作,构造一个菱形EFGH(不同于第(1)题中的特殊图形),使菱形的四个顶点分别落在矩形ABCD的四条边上(E、F、G、H分别在边AB、BC、CD、DA上,且不与矩形ABCD的顶点重合).
①请简述操作的方法,并在图3中画出菱形EFGH.
②求菱形EFGH的面积的取值范围.

考点:四边形综合题,全等三角形的判定与性质,勾股定理,菱形的判定与性质,矩形的性质,圆周角定理,轴对称的性质,锐角三角函数的定义
专题:综合题
分析:(1)如图1,由折叠可得HF=AB=24,GE=BC=10,然后运用菱形的面积公式就可解决问题.
(2)如图2,由折叠可得EF⊥AC,OA=OC;由矩形ABCD可得DC∥AB,从而有∠ECO=∠FAO,进而可证到△EOC≌△FOA,则有OE=OF,就可证到四边形AECF是菱形.
(3)①只需先通过折叠找到矩形的中心0,然后再经过两次折叠(两条折痕过点O且互相垂直)就可得到符合要求的菱形EFGH;
②易证∠GDH=∠GOH=90°,从而可得O、G、D、H四点共圆,根据圆周角定理可得∠GHO=∠GDO,然后利用三角函数就可得到
=
=
.设OG=5k,则OH=12k,从而得到菱形EFGH的面积为120k2.只需求出k的范围,就可解决问题.
(2)如图2,由折叠可得EF⊥AC,OA=OC;由矩形ABCD可得DC∥AB,从而有∠ECO=∠FAO,进而可证到△EOC≌△FOA,则有OE=OF,就可证到四边形AECF是菱形.
(3)①只需先通过折叠找到矩形的中心0,然后再经过两次折叠(两条折痕过点O且互相垂直)就可得到符合要求的菱形EFGH;
②易证∠GDH=∠GOH=90°,从而可得O、G、D、H四点共圆,根据圆周角定理可得∠GHO=∠GDO,然后利用三角函数就可得到
| OG |
| OH |
| BC |
| DC |
| 5 |
| 12 |
解答:解:(1)如图1,
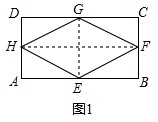
由折叠可得:HF=AB=24,GE=BC=10.
∴S菱形EFGH=
HF•GE=
×24×10=120.
∴菱形EFGH的面积为120cm2.
(2)证明:如图2,

由折叠可得:EF⊥AC.OA=OC.
∵四边形ABCD是矩形,
∴DC∥AB.
∴∠ECO=∠FAO.
在△EOC和△FOA中,
.
∴△EOC≌△FOA(ASA).
∴OE=OF.
∵OE=OF,OC=OA,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴平行四边形AECF是菱形.
(3)①将矩形纸片分别沿着AC、BD折叠,设两折痕的交点为0,展开后沿经过点O的线FH折叠,
展开后再沿经过点O且与FH垂直的线EG折叠,则图3中的四边形EFGH就是符合要求的菱形EFGH.

②∵四边形ABCD是矩形,四边形EFGH是菱形,
∴∠GDH=∠GOH=90°.
∴O、G、D、H四点共圆.
∴∠GHO=∠GDO.
∴tan∠GHO=tan∠GDO.
∴
=
=
=
.
设OG=5k,则OH=12k.
∴FH=24k,GE=10k.
∴S菱形EFGH=
FH•GE=120k2.
在Rt△ABC中,
AC=
=
=26.
∴OA=
AC=13.
当OH⊥AD时,OH=
AB=12.
∴12<OH<13.
∴12<12k<13.
∴1<k<
.
∴1<k2<
.
∴120<120k2<
.
∴120<S菱形EFGH<
.
即菱形EFGH的面积大于120cm2且小于
cm2.

由折叠可得:HF=AB=24,GE=BC=10.
∴S菱形EFGH=
| 1 |
| 2 |
| 1 |
| 2 |
∴菱形EFGH的面积为120cm2.
(2)证明:如图2,

由折叠可得:EF⊥AC.OA=OC.
∵四边形ABCD是矩形,
∴DC∥AB.
∴∠ECO=∠FAO.
在△EOC和△FOA中,
|
∴△EOC≌△FOA(ASA).
∴OE=OF.
∵OE=OF,OC=OA,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴平行四边形AECF是菱形.
(3)①将矩形纸片分别沿着AC、BD折叠,设两折痕的交点为0,展开后沿经过点O的线FH折叠,
展开后再沿经过点O且与FH垂直的线EG折叠,则图3中的四边形EFGH就是符合要求的菱形EFGH.

②∵四边形ABCD是矩形,四边形EFGH是菱形,
∴∠GDH=∠GOH=90°.
∴O、G、D、H四点共圆.
∴∠GHO=∠GDO.
∴tan∠GHO=tan∠GDO.
∴
| OG |
| OH |
| BC |
| DC |
| 10 |
| 24 |
| 5 |
| 12 |
设OG=5k,则OH=12k.
∴FH=24k,GE=10k.
∴S菱形EFGH=
| 1 |
| 2 |
在Rt△ABC中,
AC=
| AB2+BC2 |
| 242+102 |
∴OA=
| 1 |
| 2 |
当OH⊥AD时,OH=
| 1 |
| 2 |
∴12<OH<13.
∴12<12k<13.
∴1<k<
| 13 |
| 12 |
∴1<k2<
| 169 |
| 144 |
∴120<120k2<
| 845 |
| 6 |
∴120<S菱形EFGH<
| 845 |
| 6 |
即菱形EFGH的面积大于120cm2且小于
| 845 |
| 6 |
点评:本题考查了轴对称的性质、矩形的性质、菱形的判定与性质、菱形的面积公式、全等三角形的判定与性质、勾股定理、圆周角定理、三角函数等知识,综合性强,还考查了操作、推理、探究等能力,是一道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
菱形的两条对角线的长分别是6和8,则这个菱形的面积是( )
| A、20 | B、24 | C、48 | D、50 |
 如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE.求∠EBD的度数.
如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE.求∠EBD的度数. 将-8,-6,-4,-2,0,2,4,6,8这9个数分别填如图的9个空格中,使得横,竖,斜对角的3个数相加的和为0,怎么填?
将-8,-6,-4,-2,0,2,4,6,8这9个数分别填如图的9个空格中,使得横,竖,斜对角的3个数相加的和为0,怎么填?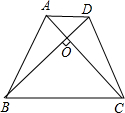 如图所示,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,AB+BC=18,求梯形ABCD的高.
如图所示,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,AB+BC=18,求梯形ABCD的高.