��Ŀ����
2��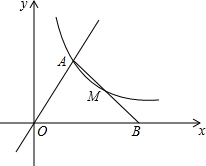 ��ƽ��ֱ������ϵ�У���֪��һ�����ڵĵ�A������Ϊ��1��m����OA=2������������y=$\frac{3x}{m}$�ͷ���������y=$\frac{k-1}{x}$��ͼ������A����A��OA�Ĵ��߽�x���ڵ�B��
��ƽ��ֱ������ϵ�У���֪��һ�����ڵĵ�A������Ϊ��1��m����OA=2������������y=$\frac{3x}{m}$�ͷ���������y=$\frac{k-1}{x}$��ͼ������A����A��OA�Ĵ��߽�x���ڵ�B����1����m��k��ֵ��
��2�����B�����ꣻ
��3��������ƽ���ڣ�ȡMΪ�߶�AB���е㣮��ABΪ�ױ��ڡ�ABO���ⲿ������������ABC����ֱ��MC���OA�к���λ�ù�ϵ��֤����Ľ��ۣ�
���� ��1�����ô���ϵ������A�������������������ʽ�����ó�m��ֵ�����ɵó�A�����꣬�ٽ�A����뷴������������ʽ���ɵó�k��ֵ��
��2��������֪�������AO�Ľ���ʽ�����������AB�Ľ���ʽ���ͼ����x�ύ�㼴�ɣ�
��3�����õ��������ε����ʽ�ϴ��ߵ����ʵó��𰸣�
���  �⣺��1���ߵ�һ�����ڵĵ�A������Ϊ��1��m����������������y=$\frac{3x}{m}$��ͼ���ϣ�
�⣺��1���ߵ�һ�����ڵĵ�A������Ϊ��1��m����������������y=$\frac{3x}{m}$��ͼ���ϣ�
��m=$\frac{3��1}{m}$��
��ã�m=��$\sqrt{3}$��
������������������һ�������ޣ�
��m=$\sqrt{3}$��
��A��1��$\sqrt{3}$��������y=$\frac{k-1}{x}$��k-1=$\sqrt{3}$��
��k=$\sqrt{3}$+1��
��2����m=$\sqrt{3}$��
��ֱ��OA�Ľ���ʽΪ��y=$\sqrt{3}$x��
�߹�A��OA�Ĵ��߽�x���ڵ�B��
��ֱ��AB�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+b��
��A�����ֱ��AB�Ľ���ʽ�ã�$\sqrt{3}$=-$\frac{\sqrt{3}}{3}$+b
��ã�b=$\frac{4\sqrt{3}}{3}$��
��ֱ��AB�Ľ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$��
��y=0����ã�x=4��
��B��$\frac{4\sqrt{3}}{3}$��0����
��3��CM��AO��
���ɣ���MΪ�߶�AB���е㣮��ABΪ�ױ��ڡ�ABO���ⲿ������������ABC��
��CM��AB��
�֡�OA��AB��
��CM��AO��
���� ������Ҫ�����˷����������ۺ��Լ�����ϵ������һ�κ�������ʽ�Լ����������ε����ʵ�֪ʶ����ȷ���ֱ��AB�Ľ���ʽ�ǽ���ؼ���

 ��ͼ��ʾ��ij����һ��ʯ������Բ���Σ��ӻ���������Ϊ12m�����İ뾶Ϊ10m����Ϊ��������
��ͼ��ʾ��ij����һ��ʯ������Բ���Σ��ӻ���������Ϊ12m�����İ뾶Ϊ10m����Ϊ��������| A�� | 3m | B�� | 2m | C�� | 4m | D�� | $\sqrt{3}$m |
| A�� | ��0��0�� | B�� | ��-1��0�� | C�� | ��0��1�� | D�� | ��0��-1�� |