题目内容
14．若$\frac{2}{x}$=$\frac{3}{y}$=$\frac{5}{z}$，且3x+2y-z=14，求x，y，z的值．分析 利用比例性质得到$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{5}$，可设$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{5}$=t，得到x=2t，y=3t，z=5t，把x=2t，y=3t，z=5t代入3x+2y-z=14中可求出t的值，从而可得到x，y，z的值．
解答 解：∵$\frac{2}{x}$=$\frac{3}{y}$=$\frac{5}{z}$，
∴$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{5}$，
设$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{5}$=t，则x=2t，y=3t，z=5t，
∵3x+2y-z=14，
∴6t+6t-5t=14，解得t=2，
∴x=4，y=6，z=10．
点评 本题考查了比例的性质：内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质．
练习册系列答案
相关题目
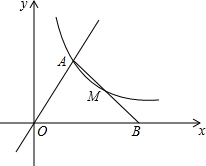在平面直角坐标系中，已知第一象限内的点A的坐标为（1，m），OA=2，正比例函数y=$\frac{3x}{m}$和反比例函数y=$\frac{k-1}{x}$的图象都经过点A，过A作OA的垂线交x轴于点B．
3．下列说法正确的是（ ）
| A． | $\frac{x-2}{3}$是分式 | B． | 分式的分子为0，则分式的值为0 | ||
| C． | 将式子（a+b）÷c写成分数的形式是a+$\frac{b}{c}$ | D． | 对于任意实数，$\frac{x}{1+{x}^{2}}$总有意义 |
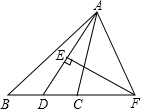如图，AD平分∠BAC，EF垂直平分AD交BC的延长线于F，连接AF．试判断∠B与∠CAF的大小关系，并说明理由．