题目内容
11.已知抛物线y=-3(x-2)2-5,解决下列问题:(1)将抛物线y=-3x2经过怎样的平移才能得到抛物线y=-3(x-2)2-5?
(2)写出抛物线y=-3(x-2)2-5的顶点坐标和对称轴;
(3)当x在什么范围内时,函数y=-3(x-2)2-5的函数值y随x的增大而减小?
分析 (1)找到两个抛物线的顶点,根据抛物线的顶点即可判断是如何平移得到.
(2)已知抛物线解析式为顶点式,可直接写出顶点坐标和对称轴.
(3)因为a=-3<0,抛物线开口向下,在对称轴右侧,y随x的增大而减小.
解答 解:(1)∵y=-3(x-2)2-5的顶点坐标为(2,-5),y=-3x2的顶点坐标为(0,0),
∴将抛物线y=-3x2向右平移2个单位,再向下平移5个单位,可得到抛物线y=-3(x-2)2-5.
(2)∵y=-3(x-2)2-5为抛物线解析式的顶点式,
∴抛物线的顶点坐标为(2,-5),对称轴是直线x=2.
(3)∵a=-3<0,
∴二次函数的开口向下,
∴当x>2时,y随x增大而减小.
点评 本题主要考查了二次函数的图象与几何变换以及二次函数的性质,应熟记二次函数的顶点坐标公式及对称轴公式,体现了数形结合思想.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | $\frac{x-2}{3}$是分式 | B. | 分式的分子为0,则分式的值为0 | ||
| C. | 将式子(a+b)÷c写成分数的形式是a+$\frac{b}{c}$ | D. | 对于任意实数,$\frac{x}{1+{x}^{2}}$总有意义 |
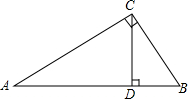 如图,Rt△ABC中,CD是斜边AB上的高.求证:
如图,Rt△ABC中,CD是斜边AB上的高.求证: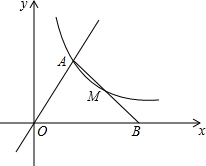 在平面直角坐标系中,已知第一象限内的点A的坐标为(1,m),OA=2,正比例函数y=$\frac{3x}{m}$和反比例函数y=$\frac{k-1}{x}$的图象都经过点A,过A作OA的垂线交x轴于点B.
在平面直角坐标系中,已知第一象限内的点A的坐标为(1,m),OA=2,正比例函数y=$\frac{3x}{m}$和反比例函数y=$\frac{k-1}{x}$的图象都经过点A,过A作OA的垂线交x轴于点B.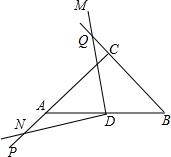 在△ABC中,∠A=∠B=α,点D为AB中点,∠MDN=2α,当∠MDN绕点D旋转的过程中,DN交AC于点P,DM交BC于点Q,探究DP,DQ的数量关系,并证明.
在△ABC中,∠A=∠B=α,点D为AB中点,∠MDN=2α,当∠MDN绕点D旋转的过程中,DN交AC于点P,DM交BC于点Q,探究DP,DQ的数量关系,并证明.