题目内容
3.已知1+a3+a6+…+a2013=0,求1+a+a2+a3+…+a2015的值.分析 把每三项作为一组,利用分组分解法得到1+a+a2+a3+…+a2015=(1+a+a2)+a3(1+a+a2)+a6(1+a+a2)+…+a2013(1+a+a2)=(1+a+a2)(1+a3+a6+…+a2013),再将1+a3+a6+…+a2013=0代入,即可求解.
解答 解:∵1+a3+a6+…+a2013=0,
∴1+a+a2+a3+…+a2015
=(1+a+a2)+a3(1+a+a2)+a6(1+a+a2)+…+a2013(1+a+a2)
=(1+a+a2)(1+a3+a6+…+a2013)
=0.
点评 本题考查了因式分解的应用:利用因式分解解决求值问题.因式分解是研究代数式的基础,通过因式分解将多项式合理变形,是求代数式值的常用解题方法,具体做法是:根据题目的特点,先通过因式分解将式子变形,然后再进行整体代入.用因式分解的方法将式子变形时,根据已知条件,变形的可以是整个代数式,也可以是其中的一部分.

练习册系列答案
相关题目
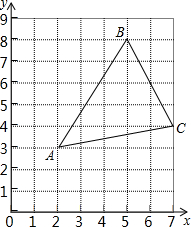 如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.
如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.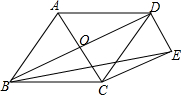 如图,已知?ABCD的对角线AC和BD交于点O,∠BAC=∠BCA,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,已知?ABCD的对角线AC和BD交于点O,∠BAC=∠BCA,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.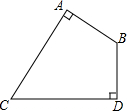 如图,四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,AB=4,CD=4$\sqrt{3}$,则该四边形的面积是16$\sqrt{3}$.
如图,四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,AB=4,CD=4$\sqrt{3}$,则该四边形的面积是16$\sqrt{3}$.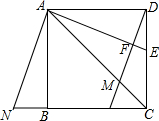 已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.
已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.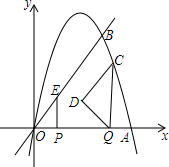 如图,抛物线y=-x2+6x与x轴交于O,A两点,与直线y=2x交于O,B两点.点P在线段OA上以每秒1个单位的速度从点O向终点A运动,作EP⊥x轴交直线OB于E;同时在线段OA上有另一个动点Q,以每秒1个单位的速度从点A向点O运动(不与点O重合).作CQ⊥x轴交抛物线于点C,以线段CQ为斜边作如图所示的等腰直角△CQD.设运动时间为t秒.
如图,抛物线y=-x2+6x与x轴交于O,A两点,与直线y=2x交于O,B两点.点P在线段OA上以每秒1个单位的速度从点O向终点A运动,作EP⊥x轴交直线OB于E;同时在线段OA上有另一个动点Q,以每秒1个单位的速度从点A向点O运动(不与点O重合).作CQ⊥x轴交抛物线于点C,以线段CQ为斜边作如图所示的等腰直角△CQD.设运动时间为t秒.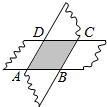 如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是平行四边形.
如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是平行四边形.