题目内容
11.若n为自然数,2n-2-n=6,求4n+4-n的值.分析 根据2n-2-n=6,可得2n-$\frac{1}{{2}^{n}}$=6,再两边同时平方可得22n+$\frac{1}{{2}^{2n}}$-2=36,进而可得4n+$\frac{1}{{4}^{n}}$=38,变形可得4n+4-n=38.
解答 解:∵2n-2-n=6,
∴2n-$\frac{1}{{2}^{n}}$=6,
∴(2n-$\frac{1}{{2}^{n}}$)2=62,
22n+$\frac{1}{{2}^{2n}}$-2=36,
∴4n+$\frac{1}{{4}^{n}}$=38,
∴4n+4-n=38.
点评 此题主要考查了负整数指数幂,以及完全平方公式,关键是掌握a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
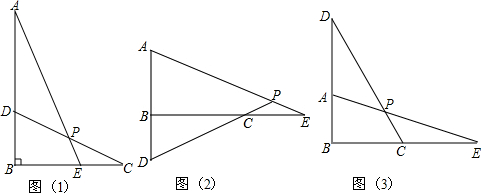
1. 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )| A. | 圆锥的底面半径为3 | B. | tanα=$\frac{\sqrt{2}}{2}$ | ||
| C. | 圆锥的表面积为12π | D. | 该圆锥的主视图的面积为8$\sqrt{2}$ |
6.已知3x=5,9y=10,则3x+2y=( )
| A. | 50 | B. | -100 | C. | 100 | D. | 无法确定 |
10.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2-2b2,则( )
| A. | △ABC是直角三角形,且∠A为直角 | B. | △ABC是直角三角形,且∠B为直角 | ||
| C. | △ABC是直角三角形,且∠C为直角 | D. | △ABC不是直角三角形 |
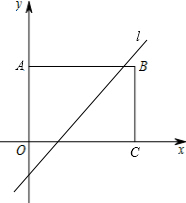 如图,矩形OABC中,A、C分别是y轴、x轴上的点,且OA=3,OC=4,将矩形OABC沿直线l折叠,使A点与C点重合,则直线l的解析式为y=$\frac{4}{3}x$-$\frac{7}{6}$.
如图,矩形OABC中,A、C分别是y轴、x轴上的点,且OA=3,OC=4,将矩形OABC沿直线l折叠,使A点与C点重合,则直线l的解析式为y=$\frac{4}{3}x$-$\frac{7}{6}$.