题目内容
18.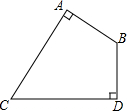 如图,四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,AB=4,CD=4$\sqrt{3}$,则该四边形的面积是16$\sqrt{3}$.
如图,四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,AB=4,CD=4$\sqrt{3}$,则该四边形的面积是16$\sqrt{3}$.
分析 延长CA、DB交于点E,则∠C=60°,∠E=30°.在Rt△ABE中,利用含30°角的直角三角形的性质求出BE=2AB=8,根据勾股定理求出AE=4$\sqrt{3}$.同理,在Rt△DEC中求出CE=2CD=8$\sqrt{3}$,DE=$\sqrt{C{E}^{2}-C{D}^{2}}$=12,然后根据S四边形ABDC=S△CDE-S△ABE,计算即可求解.
解答 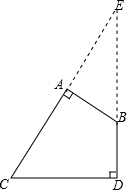 解:如图,延长CA、DB交于点E,
解:如图,延长CA、DB交于点E,
∵四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,
∴∠C=60°,
∴∠E=30°.
在Rt△ABE中,∵AB=4,∠E=30°,
∴BE=2AB=8,
∴AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=4$\sqrt{3}$.
在Rt△DEC中,∵∠E=30°,CD=4$\sqrt{3}$,
∴CE=2CD=8$\sqrt{3}$,
∴DE=$\sqrt{C{E}^{2}-C{D}^{2}}$=12,
∴S△ABE=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$,
S△CDE=$\frac{1}{2}$×4$\sqrt{3}$×12=24$\sqrt{3}$,
∴S四边形ABDC=S△CDE-S△ABE=16$\sqrt{3}$.
故答案为16$\sqrt{3}$.
点评 本题考查了勾股定理,含30°角的直角三角形的性质,图形的面积,准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
6.已知3x=5,9y=10,则3x+2y=( )
| A. | 50 | B. | -100 | C. | 100 | D. | 无法确定 |
16.设O是等边三角形ABC内一点,已知∠AOB=130°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
| A. | 65° | B. | 60° | C. | 45° | D. | 70° |
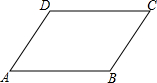 已知:如图,AB∥CD,∠A=∠C,求证:∠B=∠D.
已知:如图,AB∥CD,∠A=∠C,求证:∠B=∠D. 有一个直径为a+b的圆形公园,挖去直径分别为a与b的两个圆形荷花池,剩下的地方全部植草皮,问草皮的面积是多少?
有一个直径为a+b的圆形公园,挖去直径分别为a与b的两个圆形荷花池,剩下的地方全部植草皮,问草皮的面积是多少?