题目内容
2．
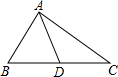如图，在Rt△ABC中，∠BAC=90°，AB=6，D是斜边BC的中点，若AD=5，则AC等于（ ）| A． | 8 | B． | 64 | C． | 5$\sqrt{2}$ | D． | 6$\sqrt{3}$ |
分析 根据直角三角形斜边上中线性质求出BC，根据勾股定理求出AC即可．
解答 解：∵在Rt△BAC中，∠BAC=90°，D为斜边BC的中点，AD=5，
∴BC=2AD=10，
由勾股定理得：AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
故选A．
点评 本题考查了勾股定理，直角三角形斜边上中线性质的应用，能求出BC的长是解此题的关键，注意：直角三角形斜边上的中线等于斜边的一半．
练习册系列答案
相关题目
如图，线段AB，CD相交于点O，OT⊥AB于O，CE∥AB交CD于点C．若∠ECO=30°，则∠DOT等于60°．
10．在2010年广州亚运会上，中国男篮勇夺金牌，12名男篮队员年龄情况如下表，则这批队员年龄的众数和中位数是（ ）
| 年龄（单位：岁） | 17 | 20 | 23 | 27 | 30 | 33 |
| 人 数 | 1 | 2 | 2 | 4 | 2 | 1 |
| A． | 27，23 | B． | 27，27 | C． | 27，25 | D． | 27，28.5 |
17．数据10，15，15，20，40的众数是（ ）
| A． | 15 | B． | 17.5 | C． | 20 | D． | 40 |
7．
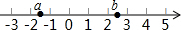实数a、b在数轴上的位置如图，则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{（a-b）^{2}}$的结果是（ ）
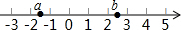实数a、b在数轴上的位置如图，则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{（a-b）^{2}}$的结果是（ ）| A． | 0 | B． | -2a | C． | 2b | D． | -2a+2b |
几何证明．