题目内容
13.从-2,-1,1三个数中任取一个,作为反比例函数y=$\frac{k}{x}$的k值,则所得反比例函数中y随x的增大而增大的概率是$\frac{2}{3}$.分析 根据反比例函数的性质可知,图象在每个象限内y随x的增大而增大,则比例系数小于0,从而从三个数中确定满足条件的数,然后利用概率公式即可.
解答 解:∵反比例函数y=$\frac{k}{x}$的图象在其象限内y的值随x值的增大而增大,
∴k<0,
∴满足条件的k的值有-2,-1,
∴使得反比例函数中y随x的增大而增大的概率为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
3.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
(不考虑除进价之外的其它费用)
(1)如果商店将购进的电视机与洗衣机销售完毕后获得利润为y元,购进电视机x台,求y与x的函数关系式(利润=售价-进价)
(2)请你帮助商店算一算有多少种进货方案?
(3)哪种进货方案待商店将购进的电视机与洗衣机销售完毕后获得利润最多?并求出最多利润.
| 类 别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
(不考虑除进价之外的其它费用)
(1)如果商店将购进的电视机与洗衣机销售完毕后获得利润为y元,购进电视机x台,求y与x的函数关系式(利润=售价-进价)
(2)请你帮助商店算一算有多少种进货方案?
(3)哪种进货方案待商店将购进的电视机与洗衣机销售完毕后获得利润最多?并求出最多利润.
8.在某次体育活动中,统计九年级1,2班学生每分钟跳绳的成绩(单位:次)情况如表:下面3种说法错误的是( )
①1班学生的平均成绩高于2班学生的平均成绩
②1班学生成绩的波动比2班学生成绩的波动小
③1班学生成绩优秀的人数(跳绳次数≥150)不会多于2班学生成绩优秀的人数.
| 参加人数 | 平均次数 | 中位数 | 方差 | |
| 1班 | 50 | 135 | 151 | 110 |
| 2班 | 50 | 135 | 149 | 190 |
②1班学生成绩的波动比2班学生成绩的波动小
③1班学生成绩优秀的人数(跳绳次数≥150)不会多于2班学生成绩优秀的人数.
| A. | ① | B. | ② | C. | ③ | D. | ①和③ |
2.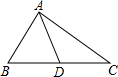 如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )
如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )
 如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )
如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )| A. | 8 | B. | 64 | C. | 5$\sqrt{2}$ | D. | 6$\sqrt{3}$ |