题目内容
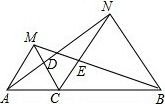 如图,点C为线段AB上一点,△ACM、△BCN是两个等边三角形,连接AN交CM于D,连接BM交CN于E,求证:CD=CE.
如图,点C为线段AB上一点,△ACM、△BCN是两个等边三角形,连接AN交CM于D,连接BM交CN于E,求证:CD=CE.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:由等边三角形可得其对应线段相等,对应角相等,进而可由SAS得到△CAN≌△MCB,于是∠CMB=∠CAN,再根据ASA可得△ACD≌△MCE,结论得证.
解答:解:∵△ACM,△CBN是等边三角形,
∴AC=MC,BC=NC,∠ACM=60°,∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,
即:∠ACN=∠MCB,
在△CAN和△MCB中,
,
∴△CAN≌△MCB(SAS),
∴∠CMB=∠CAN
又∵∠ACM=∠MCN=60°,AC=MC
在△ACD和△MCE中,
,
△ACD≌△MCE(ASA),
∴CD=CF.
∴AC=MC,BC=NC,∠ACM=60°,∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,
即:∠ACN=∠MCB,
在△CAN和△MCB中,
|
∴△CAN≌△MCB(SAS),
∴∠CMB=∠CAN
又∵∠ACM=∠MCN=60°,AC=MC
在△ACD和△MCE中,
|
△ACD≌△MCE(ASA),
∴CD=CF.
点评:本题主要考查了全等三角形的判定及性质以及等边三角形的判定问题,能够掌握并熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③x2+2x-3;④3x2-
=0.
①3x2+7=0;②ax2+bx+c=0;③x2+2x-3;④3x2-
| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
 在△ABC中,点D、E分别在AB、AC上,DE∥BC,AD=CE.若
在△ABC中,点D、E分别在AB、AC上,DE∥BC,AD=CE.若 如图,P为等边△ABC内任一点,设PA=x,PB=y,PC=z,AB=a.求证:x+y+z<2a.
如图,P为等边△ABC内任一点,设PA=x,PB=y,PC=z,AB=a.求证:x+y+z<2a. 如图,长方形的宽是a,则阴影部分的面积是
如图,长方形的宽是a,则阴影部分的面积是