题目内容
对角线长为2的正方形的周长为 ,面积为 .
考点:正方形的性质
专题:
分析:在直角△ABC中,∠ABC=90°,即AC为斜边,且AB=BC即可求AB的值,根据周长为4个边长,面积为边长的平方即可解题.
解答:解:设AB=x,则BC=x,
在直角△ABC中,∠ABC=90°,即AC为斜边,
∴AB2+BC2=AC2,故2x2=4,
即x=
,
所以正方形ABCD的周长为4x=4
,
正方形ABCD的面积为S=AB2=2,
答:正方形ABCD的周长为4
,面积为2.
故答案为4
,2.
在直角△ABC中,∠ABC=90°,即AC为斜边,
∴AB2+BC2=AC2,故2x2=4,
即x=
| 2 |
所以正方形ABCD的周长为4x=4
| 2 |
正方形ABCD的面积为S=AB2=2,
答:正方形ABCD的周长为4
| 2 |
故答案为4
| 2 |
点评:本题考查了勾股定理在直角三角形中的运用,考查了正方形各边长相等、各内角均为直角的性质,本题中正确的计算AB是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,有一块边长为(3a+2)米的正方形铁片,王师傅要制作一个工件,欲在正方形铁片中央剪去一个小正方形铁片,按照图纸要求剪去小正方形后工件的宽度为2b米.问剪去小正方形后工件的面积是多少?
如图,有一块边长为(3a+2)米的正方形铁片,王师傅要制作一个工件,欲在正方形铁片中央剪去一个小正方形铁片,按照图纸要求剪去小正方形后工件的宽度为2b米.问剪去小正方形后工件的面积是多少? 如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点D的坐标是
如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点D的坐标是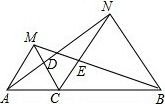 如图,点C为线段AB上一点,△ACM、△BCN是两个等边三角形,连接AN交CM于D,连接BM交CN于E,求证:CD=CE.
如图,点C为线段AB上一点,△ACM、△BCN是两个等边三角形,连接AN交CM于D,连接BM交CN于E,求证:CD=CE. 如图,ABCD是一个正方形,△APM的面积是15,CNR的面积是12,四边形PQRD的面积是51,则四边形BMQN的面积是
如图,ABCD是一个正方形,△APM的面积是15,CNR的面积是12,四边形PQRD的面积是51,则四边形BMQN的面积是