题目内容
 如图,长方形的宽是a,则阴影部分的面积是
如图,长方形的宽是a,则阴影部分的面积是考点:列代数式,代数式求值
专题:
分析:利用扇形面积求法以及弧长公式分别得出即可.
解答:解:由图形可得出:长方形的长是2a,
则阴影部分的面积是:2a2-
πa2=(2-
π)a2
阴影部分的周长是:a+a+2a+πa=4a+πa=(4+π)a,
当a=2时,阴影部分的面积是:(2-
π)a2=(2-
π)×22=8-2π,
阴影部分的周长是:8+2π.
故答案为:(2-
π)a2,(4+π)a,8-2π,8+2π.
则阴影部分的面积是:2a2-
| 1 |
| 2 |
| 1 |
| 2 |
阴影部分的周长是:a+a+2a+πa=4a+πa=(4+π)a,
当a=2时,阴影部分的面积是:(2-
| 1 |
| 2 |
| 1 |
| 2 |
阴影部分的周长是:8+2π.
故答案为:(2-
| 1 |
| 2 |
点评:此题主要考查了列代数式以及代数式求值,熟练应用扇形面积公式是解题关键.

练习册系列答案
相关题目
若一个多边形的内角和等于1080°,则这个多边形的对角线条数是( )
| A、10 | B、15 | C、20 | D、25 |
 如图,有一块边长为(3a+2)米的正方形铁片,王师傅要制作一个工件,欲在正方形铁片中央剪去一个小正方形铁片,按照图纸要求剪去小正方形后工件的宽度为2b米.问剪去小正方形后工件的面积是多少?
如图,有一块边长为(3a+2)米的正方形铁片,王师傅要制作一个工件,欲在正方形铁片中央剪去一个小正方形铁片,按照图纸要求剪去小正方形后工件的宽度为2b米.问剪去小正方形后工件的面积是多少?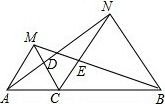 如图,点C为线段AB上一点,△ACM、△BCN是两个等边三角形,连接AN交CM于D,连接BM交CN于E,求证:CD=CE.
如图,点C为线段AB上一点,△ACM、△BCN是两个等边三角形,连接AN交CM于D,连接BM交CN于E,求证:CD=CE. 如图,ABCD是一个正方形,△APM的面积是15,CNR的面积是12,四边形PQRD的面积是51,则四边形BMQN的面积是
如图,ABCD是一个正方形,△APM的面积是15,CNR的面积是12,四边形PQRD的面积是51,则四边形BMQN的面积是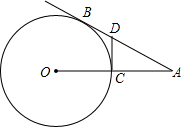 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C的切线交AB于点D.若AD=2BD,CD=2,求⊙O的半径.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C的切线交AB于点D.若AD=2BD,CD=2,求⊙O的半径.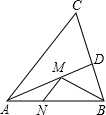 如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值?
如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值?