题目内容

在△ABC中，点D、E分别在AB、AC上，DE∥BC，AD=CE．若
AB
AC
=
3
2
，BC=10，则DE的长为
 
．
考点：相似三角形的判定与性质
专题：
分析：证出△ADE∽△ABC，推出
AB
AC
=
AD
AE
=
3
2
，
AE
AC
=
DE
BC
，求出
AE
AC
=
DE
BC
=
2
5
，代入即可求出答案．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∴
AB
AC
=
AD
AE
=
3
2
，
AE
AC
=
DE
BC
，
∵AD=CE，
∴
CE
AE
=
3
2
，
∴
AE
AC
=
DE
BC
=
2
5
，
∵BC=10，
∴DE=4，
故答案为：4．
点评：本题考查了相似三角形的性质和判定的应用，解此题的关键是求出
AE
AC
=
2
5
．
练习册系列答案
相关题目
计算题
（1）1
1
4
+（-
1
5
）-1+0.75 
（2）（-2.7）+（+1
3
5
）-（-6.7）+（-1.6）
（3）312+（-12）-（-13）+（-223）
（4）（-
3
7
）-（-
1
5
）-（-
2
7
）+（-1
1
5
）
（5）（-56）×（
4
7
-
3
8
+
1
14
）
（6）-16-（1-0.5）2×
1
5
×[2+（-3）3]．
如图，平面内，四条线段AB、BC、CD、DA首尾顺次相接，∠ABC=20°，∠ADC=40°．
（1）如图1，∠BAD和∠BCD的角平分线交于点M，求∠AMC的大小；
（2）如图2，点E在BA的延长线上，∠DAE的平分线和∠BCD的平分线交于点N，求∠ANC度数；
（3）如图3，点E在BA的延长线上，点F在BC的延长线上，∠DAE的平分线和∠DCF的平分线交于点P，请直接写出∠APC 的度数．
在抗洪抢险中，人民解放军的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：+14，-9，+8，-7，+13，-6，+10，-5．
（1）B地在A地何处？
（2）若冲锋舟每千米耗油0.5升，一天共耗油多少升？
（3）冲锋舟在当天的航行过程中离A地最远距离是多少？
如图，在正方形ABCD中，AB=2cm，对角线AC、BD交于点O，点E以一定的速度从A向B移动，点F以相同的速度从B向C移动，连结OE、OF、EF．
（1）△AOE≌△
 
；
（2）线段EF的最小值是
 
cm．
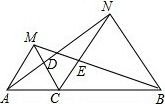如图，点C为线段AB上一点，△ACM、△BCN是两个等边三角形，连接AN交CM于D，连接BM交CN于E，求证：CD=CE．
从-55起逐次加1得到一连串整数，-54，-53，-52，…请问：
（1）第110个整数是什么？
（2）这110个整数的和是什么？
若抛物线y=-
1
2
x2沿x轴向左或向右平移后，经过点P（5，-2），求平移后的抛物线的解析式．
已知等腰三角形的周长为2+2
3
，底边上的高为1，求底角的正弦值和等腰三角形的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网