题目内容
10.在平面直角坐标系中,如果横坐标与纵坐标都是整数的点称为整点,将二次函数y=x2+6x-$\frac{27}{4}$的图象与x轴所围成的封闭图形染成红色,则在此红色区域内部及其边界上的整点的个数是( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
分析 找到函数图象与x轴的交点,那么就找到了相应的x的整数值,代入函数求得y的值,那么就求得了y的范围.
解答 解:将该二次函数化简得,y=-[(x-3)2-$\frac{9}{4}$],令y=0得,x=$\frac{9}{2}$或$\frac{3}{2}$.
则在红色区域内部及其边界上的整点为(2,0),(3,0),(4,0),(2,1),(3,1),(4,1),(3,2)七个.
故选B.
点评 本题考查了二次函数图象和性质,解决本题的关键是得到相对应的x的值.

练习册系列答案
相关题目

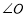 的内部有一滑动杆
的内部有一滑动杆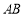 .当端点
.当端点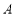 沿直线
沿直线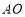 向下滑动时,端点
向下滑动时,端点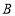 会随之自动地沿直线
会随之自动地沿直线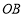 向左滑动.如果滑动杆从图中
向左滑动.如果滑动杆从图中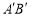 处,那么滑动杆的中点
处,那么滑动杆的中点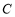 所经过的路径是( )
所经过的路径是( )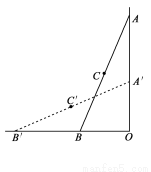
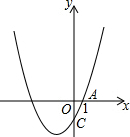 如图,抛物线y=x2+2x-3与x轴正半轴,y轴分别交于点A、C,若点P在抛物线上,且△POC的面积是△AOC的面积的4倍,求点P的坐标.
如图,抛物线y=x2+2x-3与x轴正半轴,y轴分别交于点A、C,若点P在抛物线上,且△POC的面积是△AOC的面积的4倍,求点P的坐标.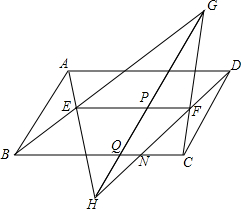 如图,已知在?ABCD内有线段EF∥BC,AE、DF的延长线交于点H,又分别交BC于点M、N,BE、CF的延长线交于点G,HG分别交EF、BC于点P、Q,求证:BQ:MQ=CQ:NQ.
如图,已知在?ABCD内有线段EF∥BC,AE、DF的延长线交于点H,又分别交BC于点M、N,BE、CF的延长线交于点G,HG分别交EF、BC于点P、Q,求证:BQ:MQ=CQ:NQ.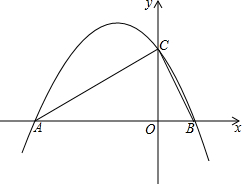 二次函数y=ax2+bx+c的图象与x轴交于点A(-8,0),B(2,0),y轴交于点C,∠ACB=90°.
二次函数y=ax2+bx+c的图象与x轴交于点A(-8,0),B(2,0),y轴交于点C,∠ACB=90°. 如图,已知AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD与AC交于E.求证:DC2=DE•DB.
如图,已知AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD与AC交于E.求证:DC2=DE•DB.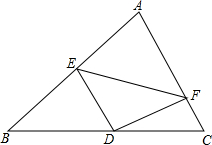 如图,△ABC中,E,F分别在AB,AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.
如图,△ABC中,E,F分别在AB,AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.